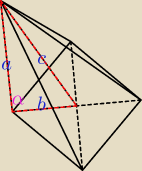
? Kone: Dany jest ostrosłup prawidłowy czworokątny o objętości 48cm². Ściana boczna jest nachylona do

	4
podstawy pod takim kątem α,że tgα=		. Wyznacz pole powierzchni bocznej tego ostrosłupa.
	3

Obliczenia: V=48cm²

	4		a
tgα=		=
	3		b

	1
a=4 , b=		3√2=1,5√2
	2

a²+b²+c² 4²+(1.5√2)²=c² 16+4,5=c² c²=20,5 c=4,52 c=h P_podstawy=3²=9 Pc=P_p=P_b // P_p

	Pc
Pb=
	Pp

Nie wiem czy to dobrze zaczęłam, czy ktoś może pokierować mnie co dalej

Kone: Nikt nie wie ?

Kone:

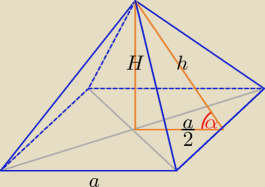Bogdan: Nie można lekceważyć jakości rysunku. Rysunek jest nie tylko elementem wspomagającym zrozumienie i zapisanie rozwiązania zadania, ale ma wpływ na estetykę pracy.

H		4		4		a		2
	=		⇒ H =		*		=		a
a   2		3		3		2		3

	1		1		2		2
48 =		a2 * H ⇒ 48 =		a2 *		a ⇒ 48 =		a3 ⇒ a = ...
	3		3		3		9

h = √H² + (a/2)²

	1
Pole powierzchni bocznej PB = 4*		ah = 2ah
	2

Kone:

	48
Czyli a=(		) 13 ?
	29

Bogdan:

	2		9
48 =		a3 / *		⇒ a3 = 216 ⇒ a = 3√216 = 6
	9		2

paka: Jest możliwa taka wersja tego zadanka? tgα=3/4 z tego : H=4 1/2a=3 a=6 h obliczam z Pitagorasa h²=H²+1/2a² h²=25 h=√25=5 Pole P=4 x 1/2 x a x h P=4 x 1/2 x 6 x 5 P=60 (cm²)