:) M4ciek: Suma dlugosci wszystkich krawedzi prostopadloscianu o podstawie kwadratowej jest rowna 64.Wykaz,ze sposrod prostopadloscianow o podanej wlasnosci najwieksze pole powierzchni calkowitej ma szescian. No to z zadania wycisnalem tyle : Prostopadloscian: 8a + 4b = 64 2a + b = 16 b = h = 16 − 2a Szescian : 12a = 64

	16
a =
	3

	16
a =
	3

	16
b = 16 − 2a ⇒ b =
	3

Czyli mam policzone boki w prostopadloscianie i szescianie. Oczywiscie jak policze pola calkowite obu bryl to beda jednakowe. Moje pytanie : Co tu teraz zrobic Pozdrawiam

M4ciek: Podbijam

Eta: P_c= 2a² +4ab , b= 16−2a , dla a€ (0,8) P_c( a)=2a² +4a(16−2a) = −6a²+64a −−− to f, kwadratowa, parabola ramionami do dołu zatem osiaga maksimum dla:

	−64		16
amax=		=
	−12		3

	16		16
bmax= 16−2*		=
	3		3

	16
zatem takim prostopadłościanem jest sześcian o krawędzi a=b=
	3

i to wszystko

M4ciek: A mozna to przedstawic bez funkcji kwadratowej

	16		16
Np. a =		podstawic do b = 16 − 2a, wyliczyc b =		i napisac ,ze
	3		3

a = b zatem prostopadloscianem jest szescian

Eta: nie Skąd wiesz,że takie pole jest maksymalne Musisz okreslić maksimum funkcji pola! 1/z funkcji kwadratowej lub 2/ z pochodnej P_c^'(a) ( ale pochodnych nie macie już w programie nauczania )

M4ciek: A w jakim celu jest przy b oznaczenie max a_max to rozumiem bo to wynika z f.kwadratowej itd. , ale z tym b_max nie do konca mi pasuje

M4ciek: Hmm Eta

Eta: b= 16 −2a b_max= 16 −2a_max

M4ciek: Hmm bo tu chodzi oto ,ze zarowno a jak i b sa potrzebne do obliczenia pola wiec obie musza byc max

Eta: i wreszcie "max" pomyślunku

M4ciek: A mam jeszcze pytanie do czegos takiego , tylko o jakas podpowiedz bym poprosil a jak nic nie wymysle to wtedy sie zglosze W trojkacie prostokatnym jedna przyprostokatna jest 3 razy dluzsza od drugiej.Wykaz ,ze wysokosc poprowadzona z wierzcholka kata prostego dzieli przeciwprostokatna na odcinki, z ktorych jeden jest 9 razy dluzszy od drugiego.

M4ciek: A i jeszcze mam takie pytanie czy: wysokosc poprowadzona z wierzcholka kata prostego na przeciwprostokatna pada pod katem prostym Mysle ,ze na 99% nie

M4ciek: Lece juz Poprosze o podpowiedz jak wpadniesz. Dobranoc

Eta: He he .... Widziałeś wysokość poprowadzoną do podstawy pod innym kątem niż prosty ( nie byłaby wysokością)

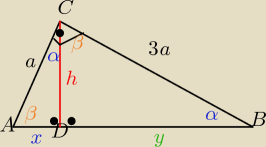
Eta: wykorzystaj podobieństwo trójkątów ΔDBC ~ ΔADC i wykaż tezę

M4ciek: ΔDBC ~ ΔADC na podstawie cechy (kkk) bo : I∠ADCI = I∠CDBI = 90^o I∠BCDI = 90^o − β Suma miar w Δ = 180^o ⇒ 90^o − β + α + 90^o = 180^o ⇒ α = β α = β ⇔ I∠ ACDI = I∠DBCI = I∠DACI = I∠DCBI Czy to tak ma byc czy wyszly glupoty

Eta: Masz wykazać,że y= 9x Użyj odpowiednich proporcji dla trójkątów podobnych i wykaż tę równość

M4ciek:

a		x + y
	=
x		a

a + 3a = x + y Takie cos

Eta: np: tak:

3a		a
	=
y		h

3ah= ay => h= ¹₃y

h		x
	=
y		h

h²= x*y

	1
		y2= x*y
	9

y= 9x c.n. u. lub tak: ΔDBC ~ ΔADC w skali k= 3

	P(ΔDBC)
to		= k2= 9
	P(ΔADC)

	y*h
P(ΔDBC)=
	2

	x*h
P(ΔADC)=
	2

to:

	y
		= 9
	x

y= 9x

M4ciek: Sprobuje swoim sposobem to jeszcze rozpisac

M4ciek: A to mozna wykorzystac dowolne boki , byle by byly proporcjonalne

M4ciek: I czy musze udowodnic ,ze te Δ sa podobne czy wystarczy ,ze napisze hmm

Eta: zaznacz kąty tak jak na rys. i z cechy (k,k,k) są podobne

M4ciek: Aha rozumiem , a z tymi bokami moge sobie pokombinowac ktore z ktorymi byle by byly proporcjonalne

Eta: tak

M4ciek: To zostawie to do jutra i zrobie od nowa po swojemu , przynajmniej sie naucze^^ bo czesto cos takiego widze ostatnimi czasy z tymi proporcjonalnymi bokami Dziekuje Eta