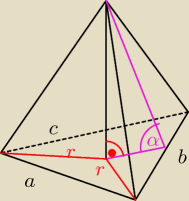
Podstawą ostrosłupa jest trójkąt o bokach a, b, c, Każda krawędź boczna jest nac bbb: Podstawą ostrosłupa jest trójkąt o bokach a, b, c, Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem α. Oblicz objętość ostrosłupa. doszedłem tylko do tego, że podstawę można wpisać w okrąg, którego środkiem jest spodek wysokości Proszę o jakieś wskazówki

bbb: up

ddd: dupacki rysunek , to krawędź jest nachylona pod kątem α, a nie ściana

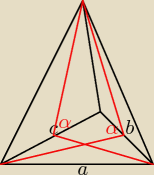bart: z tymi r sobie sam wymysliles, czy juz bylo tak w zadaniu?

ddd: Jeszcze jeden dupacki rysunek. Co jest z wami. Przecież wyraźnie jest napisane w treści zadania "każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem α". KRAWĘDŹ, a nie ściana

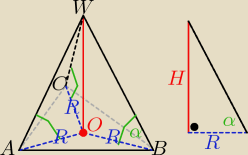Eta: Jeżeli wszystkie krawędzie boczne ostrosłupa trójkątnego tworzą z podstawą kąty o równych miarach, to spodek wysokości ostrosłupa pokrywa się ze środkiem okręgu opisanego na trójkącie( w podstawie)

	a*b*c
zatem: R=
	4PΔ

	a*b*c
to: Pp=
	4R

z trójkąta prostokątnego OBW wyznaczamy "H"ostrosłupa

	H
		= tgα
	R

H= R*tgα

	1		abc
V=		*Pp*H=		*tgα [j3]
	3		12