asymptota funkcji karola:

	x3−x
wyznacz asymptotę funkcji y=		pomóżcie jutro kolokwium
	x2−x−2

Grześ: nadal potrzebna pomoc

karola: nadal

Grześ: to już rozpisuje wszystko

Grześ:

	x3−x		x(x−1)(x+1)
y=		=		D: x∊R\{−1,2}
	x2−x−2		(x−2)(x+1)

Teraz asymptoty: Pionowa w punktach −1, 2 lecz musimy sprawdzić:

	x(x−1)(x+1)		x(x−1)		2
lim x→ −1		=lim x→ −1		= −		obustronna
	(x−2)(x+1)		(x−2)		3

asymptota pionowa w punkcie −1

	x(x−1)		2
lim x→ 2−		=		= −∞ asymptota pionowa lewostronna w punkcie 2
	(x−2)		0−

	x(x−1)		2
lim x→ 2+		=		= +∞ asymptota pionowa prawostronna w punkcie 2
	(x−2)		0+

Asymptoty ukośne o wzorze: y=ax+b Współczynniki:

	x(x−1)   (x−2)		x(x−1)
a= lim x→±∞		=		= 1
	x		x(x−2)

	x(x−1)		x2−x−x2+2x		x
b= lim x→±∞ (		− x ) =		=		= 1
	(x−2)		x−2		x−2

Czyli istnieje asymptota ukosna o wzorze: y=x+1 Asymptoty poziome nie istnieją Pozdrawiam serdecznie i powodzenia na kolokwium

karola: wielkie dzięki za rozwiązanie, teraz już będę wiedziała jak zrobić resztę pozdrawiam serdecznie

otylqa:

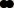
	x2−6x+3
a taki przykład y=		też na takiej zasadzie będzie liczony czy jakoś inaczej.
	x−3

bo nie wiem jak to zrobić.

Grześ: podobny, tylko asymptoty pionowe jednostronne sa w punkcie 3, Asymptoty poziome nie występują, za to istnieje asymptota skośna. Licz licz

otylqa: moze podpowiedziec jak? ;>

karola: a taka funkcja y=xarctgx w jaki sposób należy to zrobić?

Sara: a dlaczego przy x −> −1 jest liczone tylko raz i nie jest liczony punkt z prawej i lewej strony tak jak w przypadku x −> 2

Aga1.: Przy x→−1 jest liczone tylko raz ponieważ można obliczyć wartość funkcji (po skróceniu). Oczywiście nie ma asymptoty pionowej x=−1 ( bo wyszła liczba)