funkcja Oleeeek: mamy dwie funkcje f(x)=x²+3x i g(x)=2x+6 mam wyznaczyc zbior argumentow dla ktorych funkcja f przyjmuje wartosci wyzsze niz g, generalnie umiem to zrobic ale jest jedna dziwna rzecz x²+3x>2x+6 z tego wychodzi rownanie kwadrotowe x²+x−6>0 obliczylem delte i x1 i x2 wiec moge to rownanie przedstawic jako (x+3)(x−2)>0 a zatem wyszlo by x>−3 i x>2 ta druga czesc x>2 to (2, ∞) ale ta pierwsza... wiem ze powinno byc (−∞, −3) ale przeciez jezeli x jest wieksze od −3 to by wyszlo cos takiego (−3, ∞) ;\ wytlumaczcie, prosze

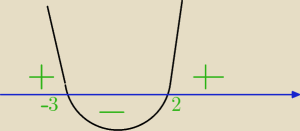
Marcin W: rozwiązanie nierówności x²+x−6>0 popatrz na rysunek wyżej to: x∊(−∞,−3)∪(2,+∞)