zad fruu: Na ostrosłupie prawidłowym czworokątnym, którego ściany boczne są nachylone do podstawy pod katem 60^o , opisano kule o polu powierzchni 16π. Oblicz pole powierzchni całkowitej tego ostrosłupa.

fruu: Zadanie z gwiazdeczką, jakieś rady ?

prawilniak: ponawiam pytanie

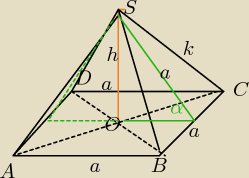
Mila: P_kuli=4πR²=16π⇔ R=2 SO zawiera się w średnicy kuli.

	a√3
h=
	2

	a√2
OC=
	2

z tw. Pitagorasa

	a√3		a√2
k2=(		)2+(		)2
	2		2

	5a2
k2=
	4

Promień kuli opisanej na tym ostrosłupie jest równy promieniowi okręgu opisanego na ΔACS Korzystając z tw. sinusów obliczymy a. Należy obliczyć sin∡ASC. w ΔASC k²=k²+k²−2*k*k*cos∡ASC. Dokończ, albo znajdź, gdzieś rozwiązane, bo już takie zadanie rozwiązywałam kilka dni temu.