Wartość bezwzględna z parametrem
Antek: Oblicz liczbę rozwiązań równania w zależności od parametru p > 0
|2x−p|+|3x−p|=8
Pomoże ktoś najlepiej krok po kroku L

17 sty 16:24
Antek: up
17 sty 16:58
Antek: straszne rzeczy
17 sty 18:48
Trivial: Nie wiem kto wymyślał zadania z parametrami. Wg mnie są one bezcelowe.
17 sty 19:10
Antek: te bez wartości bezwzględnej jeszcze ujdą ale kurde te to za cholere nie wiem jak zrobić
17 sty 19:25
Trivial:
Pewnie oczekują rozważenia dziedzin różnych itp...
Najpierw wyznaczamy przedziały metodą wykresową.
y
1 = 2x − p
y
2 = 3x − p
Miejsce zerowe dla:
17 sty 19:30
Antek: no do tego doszedłem nawet wyliczyłem parametr p dla pewnego przedziału tylko nie wiem co potem
w odpowiedz dać
17 sty 19:32
Trivial:
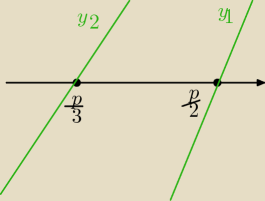
17 sty 19:33
Trivial:
Pozostało rozpisać moduły sprawdzić co i jak i pewnie coś wyjdzie.

17 sty 19:35
Eta:

17 sty 19:35
Antek: |2x+p|+|3x−p|=8 kurde powinien być + a nie minus sory
17 sty 19:36
Trivial: Moja cała ciężka praca właśnie legła w gruzach.

17 sty 19:37
Eta:
mała poprawka:

17 sty 19:37
Antek: powinno być tak
2x + p = 0
2x = − p /:2
3x−p = 0
3x = p/:3
17 sty 19:38
Trivial: | | p | |
O mam |
| ...  A czemu niby przedziały tak podomykane? Ja wolę po swojemu.  |
| | 2 | |
17 sty 19:38
Antek: To ja to napisze trivial a ty reszte wylicz

17 sty 19:38
Eta:
Antek ......... zltuj się i pisz porządnie treść zadań

!
17 sty 19:38
Trivial: Napisz dziedziny i mi narysuj, a zrobię dalej.

17 sty 19:39
Antek:
| | p | | p | | p | | p | |
przedział (−∞; − |
| > , (− |
| ; |
| > , ( |
| ;+∞) no najprostsza rzecz zrobiona co |
| | 2 | | 2 | | 3 | | 3 | |
dalej

17 sty 19:40
Antek: Eta nie bij

17 sty 19:40
Trivial: No dalej opuszczamy moduły przecież.

17 sty 19:40
Antek: No to ty zrobisz pierwszy ja drugi ok

zobaczymy czy dobrze może w ten sposób się naucze

17 sty 19:42
Trivial:
Rozważmy przedział pierwszy. Wtedy: pierwszy moduł jest ujemny, drugi też ujemny. Co dalej?

17 sty 19:42
Antek: Wyznaczamy x
17 sty 19:43
Trivial: Tak.
17 sty 19:43
Antek: Ok to napisze sprawdzisz czy dobrze będzie łątwiej
17 sty 19:43
Antek: |2x+p|+|3x−p|=8
−2x−p+p−3x=8
−5x=8
hmm co dalej

?
17 sty 19:45
Trivial: x zawsze ma rozwiązanie w tym przedziale.

17 sty 19:46
Trivial: A nieee, nie zawsze.

17 sty 19:47
Trivial: Trzeba przyrównać do dziedziny

17 sty 19:48
Antek: skąd wiesz

?
17 sty 19:48
17 sty 19:49
Trivial: Tak.
17 sty 19:50
Antek: | | 16 | |
p ≤ |
| no to w każdym przedziale analogicznie i co mam w odpowiedz wpisac  |
| | 5 | |
17 sty 19:52
Trivial: Mniej więcej analogicznie. Na końcu sumę przedziałów i powinno być OK.
17 sty 19:54
Trivial: Dla pozostałych prawdopodobnie nie ma rozw.

17 sty 19:54
Trivial: Dobra, ja uciekam... Jak nie zapomnę i jeśli jeszcze dzisiaj wejdę na forum to sprawdzę.

17 sty 19:56
Antek: muszą być bo mam 3 odpowiedzi że dwa rozwiązania dla .... jedno rozwiązanie dla.. i brak
rozwiązań dla ...

Tylko chodziło o to że ja nie wiem jak dojść do tego
17 sty 19:56
Antek: No narazie

17 sty 19:56
Trivial: mam podejrzenia, że dwa rozwiązania mogą się ujawnić w przedziale numer dwa.

17 sty 19:57
Trivial: Ale już lecę...

17 sty 19:57






 A czemu niby przedziały tak podomykane? Ja wolę po swojemu.
A czemu niby przedziały tak podomykane? Ja wolę po swojemu. 

 !
!




 zobaczymy czy dobrze może w ten sposób się naucze
zobaczymy czy dobrze może w ten sposób się naucze 

 ?
?



 ?
?



 Tylko chodziło o to że ja nie wiem jak dojść do tego
Tylko chodziło o to że ja nie wiem jak dojść do tego


