[Liczby Zespolone] Postać trygonometryczna - wyznaczanie Arg(z) radian: Witajcie! Męczę się z postacią trygonometryczną liczb zespolonych, a w szczególności z wyznaczaniem ich Argumentu. np. z = (2√3−2i)³⁰ Pomijając, że chodzi nam o 30 potęgę, aby to wyliczyć ze wzoru Moivre'a najpierw trzeba ustalić postać trygonometryczną: z = a +bi = |z|(cosφ + isinφ) Czyli dla naszego przykładu Moduł: |z| = √(2√3)² + (−2) ² = √12 + 4 = 4

	a
Znając stosunek cosφ =
	|Z|

Obliczam:

	2√3
cosφ =
	4

	√3
cosφ =
	2

	√3		π
Wszystko pięknie, cosinus ma wartość		dla φ =		, ale liczba zespolona "znajduje
	2		6

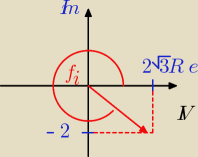
się" na wykresie w IV ćwiartce układu współrzędnych (patrz rysunek).

	3π
Jak mogę w prosty sposób znaleźć φ ? Wiem, że będzie to na pewno		+ α, gdzie α < π/2.
	2

	√3		π
Próbowałem to zrobić w taki sposób, że skoro cosφ =		, dla φ =		to dodaję "trzy
	2		6

	3π		π		10π		√2
nadmiarowe ćwiartki" i mam		+		=		. Przy cosφ =		działa, ale
	2		6		6		2

w końcu 270 stopni to nie jest okres podstawowy cosinusa... Znam wzory redukcyjne i nie wiem jak i czy mogę je tutaj zastosować. Czy da się to łatwo odczytać z wykresu ? Mam strasznie zaćmienie mózgu. Z góry dziękuję za pomoc!

radian: Ale tragicznie wyszedł opis tego pytania (wypełniłem dobrze pole Opis!). Niechcący

Jack:

	−2		1		√3
sinφ=		=−		co razem cosφ dodatnim cosφ=		daje ćwiatkę IV i kąt
	4		2		2

	π
		+3/2π
	6

radian: Dzięki za szybką odpowiedź. Czyli jednak zgadzałoby się... Czy moje myślenie jest sensowne ?

	1
Jak Ty na to spojrzałeś? Obliczyłeś sinusa i skoro wyszedł minus		to znaczy, że kąt
	2

odmierzamy w drugą stronę, a nasze φ jest 360 − 30 ? Ćwiartkę znajdę bez problemu ale zastanawiam się czy wolno mi dodawać te ćwiartki do cosφ ?

	3π
(Czyli w tym przypadku zgadzałoby się		. )
	2

W przypadku jakiejś innej wartości cosinusa dla kąta α, gdzie wiem że całe φ jest w ćwiartce np 3−ciej, byłoby to:

π
	+ α ?
2

radian: Bo głębszej analizie (matematycznej) już zrozumiałem gdzie popełniłem błąd... zamiast na siłę starać się dodać (uzupełnić) 270 stopni do 30 stopni, powinienem te 30 stopni odjąć od 360. Dzięki jeszcze raz...