nierówności, ważne! tomq: Proszę o pomoc rozwiąż nierówność:

	x2+9x+8
|		|≥1
	x2−9x+8

myślałem nad przypadkami czyli 1) x²+9x+8≥0 x²−9x+8≥0 2)x²+9x+8<0 x²−9x+8<0 3)x²+9x+8≥0 x²−9x+8<0 4)x²+9x+8<0 x²−9x+8≥0 i z tego zacząłem liczyć.. (x+8)(x+1)≥0, (x−1)(x−8)≥0 (te dwa tak wyglądają po przedstawieniu w postaci iloczynowej).. czy mógłby to ktoś jakoś szybko policzyć? Bo nie wiem, czy dobrze myślę.

czekolada: musisz rozpatrzyć 2 przypadki x<0

(−x)2−9x+8
	≥1
(−x)2+9x+8

i drugi przypadek x≥0

x2+9x+8
	≥1
x2−9x+8

i rozwiazujesz te dwa przypadki jak zwykle nierownosci. wyjda Ci dwa rozwiazania.. musisz pamietac o zalozeniach do kazdego z nich czyli to ze w jednym rozwiazanie musi byc <0 w drugim ≥0. i później połączysz dwa przedziały które Ci wyszly i to bedzie odpowiedz. i oczywiscie jeszcze założenia,że mianownik nie może być równy 0. to zanim zaczniesz rozwiązywać nierówność ; ) ale to chyba wiesz.

tomq: x≥0 18x(x−1)(x−8)≥0 x∊<0,1>U<8,∞) ale tu jeszcze założenie więc będą pootwierane x<0

x2−9x+8
	≥1
x2+9x+8

x2−9x+8−x2−9x−8
	≥0
x2+9x+8

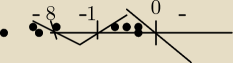
−18x(x+8)(x+1)≥0 rys. czyli x∊(−∞,−8>U<−1,0> i teraz wspólne czyli <0,1)U(8,∞) a skąd (1,8)?

tomq: odswieżam pytanie^^