Zadanie dla Godzia :))) Gustlik: Na okręgu o promieniu 1 opisano trapez równoramienny o polu 5. Oblicz: a) długości ramion trapezu b) pole czworokąta, którego wierzchołkami są punkty styczności okręgu z bokami trapezu. Miłego liczenia Myślę, Godzio, że dla Ciebie to pestka

Godzio: Już się zabieram a potem do spania

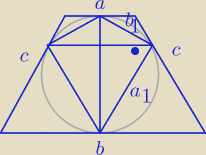
Godzio: h = 2r = 2

	a + b
P =		* h = 5 ⇒ a + b = 2,5
	2

Okrąg można wpisać w czworokąt tylko wtedy gdy a + b = c + c ⇒ 2c = 2,5 ⇒ c = 1,25 a₁² + b₂² = 2² a₁² + b₂² = 4 ⇒ (a₁ + b₂)² − 2a₁b₂ = 4 ⇒ 2,5² − 2a₁b₂ = 4 −2a₁b₂ = −2,25 a₁b₂ = 1,125

	a1b2
Pczworokąta = 2		= 1,125
	2

Trochę zajęło mi wymyślenie

Godzio: Spartoliłem a + b = 5 a dalej to już wiadomo, nie chce mi się już poprawiać

Gustlik: Ja to zrobiłem troche dłuższym sposobem: opuściłem wysokości z obu wierzchołków trapezu. Mając obliczone ramię c=2,5 i wysokość h=2 z Pitagorasa obliczyłem odcinek od spodka wysokości do wierzchołka − wyszedł on równy 1,5. Oczywiście z lewej strony jest taki sam odcinek, co daje zależność między podstawami trapezu a=b+3. Mając drugie równanie a+b=5 (z pola trapezu) obliczyłem, że a=4, b=1. Zatem punkty styczności okręgu z trapezem dzielą podstawy a i b na połowy, czyli odcinki o długościach 2 i 0,5. Z przystawania trójkątów (okrąg wpisany w kąt) wynika, że punkty te dzielą ramiona trapezu na odcinki o długościach 2 i 0,5. Poprowadziłem sobie promień ze środka okregu do punktu styczności z prawym ramieniem i wyszedł deltoid o bokach 1, 1 (promienie) oraz 2 i 2 (połowa podstawy i dłuższy fragment ramienia c) oraz o katach prostych (własność styczności okręgu i prostej). Taki deltoid jest czworokątem, który można wpisać w okrąg, zastosowałem więc wzór na pole podobny do wzoru Herona:

	1
P=√(p−a)(p−b)(p−c)(p−d), gdzie p=		obwodu czworokata.
	2

Licząc pole tego deltoidu "klasycznym" wzorem obliczyłem bok a₁, będący jego przekatną, a potem z Pitagorasa bok b₁. Majac te boki obliczyłem zadane pole czworokąta (też zresztą deltoidu) tym samym wzorem podobnym do wzoru Herona. Godzio − mam pytanie: zastanawia mnie, skąd Ty wziąłeś, że a₁+b₂=2,5? Poza tym ma być chyba b₁, a nie b₂?

Godzio: A to już całkiem mi się pogmatwało dzisiaj miałem naprawdę męczący dzień

Godzio: jutro zobacze na to zadanie i spróbuje je rozwiązać dziś już idę spać

Gustlik: Nie za bardzo mogę rysować, bo mi się komp zawiesza, dlatego starałem Ci się opisać krok po kroku, co robiłem. Jeżeli możesz, to sprawdź, bo mnie ono bardzo ciekawi, może masz jakiś inny sposób, niż mój? Bo to niezła łamigłówka, a wiem, że Ty takie lubisz. Pozdrawiam

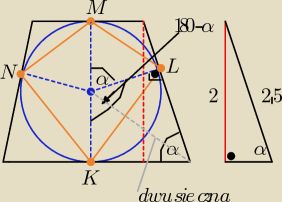
teta: Witam podaję inny sposób wyznaczenia pola czworokąta KLMN b)

	2
sinα=		= 0,8
	2,5

Czworokąt składa się z czterech trójkątów równoramiennych o ramionach r= 1 i kątach między ramionami α i 180^o −α zatem :

	1		1
P(KLMN) = 2*		*r2*sin(180o−α) +2*		*r2*sinα= 2r2*sinα= 2*1*0,8
	2		2

P(KLMN)= 1,6 [j²] pozdrawiam i życzę miłych snów

teta: I jak Gustliczku ? Myślę,że tego sposób nie zaliczysz jako ..." dookoła świata" A teraz najwyższa pora iść spać

Mateusz: teta, pomożesz mi w moich zadanqach pliiiiiiisss

teta: A co Ty? ...... z choinki się urwałeś? ....... o tej porze to już wszyscy dawno śpią Myślę,że tych zadań nie dostałeś przed sekundą mailem od Twojego nauczyciela? Sorry ...... do jutra

Mateusz: właśnie je znalazłem a ,że mam jeszcze mam nauki jakoś do 4tej więc ich nie zrobie.. szkoda, myślałem ,że dla ścisłowca nie ważne jest o której i tak zrobi w minutę.. No ale cóż eh

teta: Do Godzia 3 / sposób do b) wykorzystaj zależności między średnimi : średnią geometryczną podstawi i średnią harmoniczną podstaw trapezu

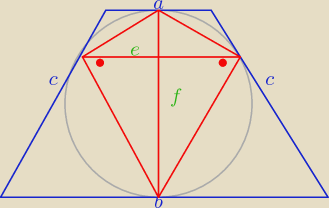
Godzio: c = 2,5 a + b = 5 r = 1 h = 2 f = 2

	2		2ab
e =		=
	1   1   + a   b		a + b

	b − a
(		)2 + h2 = c2
	2

	a + b		b − a
h2 = (		)2 − (		)2
	2		2

	a + b − b + a		a + b + b − a
h2 =		*
	2		2

	2a		2b
h2 =		*
	2		2

h² = ab ⇒ ab = 4

	2 * 4		8
e =		=
	5		5

	e * f		8
P =		=		= 1,6
	2		5

No i wyszło tylko czy jest pewność że odcinek łączący punkty styczności z ramionami to akurat średnia harmoniczna podstaw ?

Gustlik: Teta, Ty jesteś może Eta? Twój sposób jest dobry, każdy ma swój. Ja nie ganię nikogo za sposób rozwiązywania, tylko chcę zwrócić uwagę, że wiele szkolnych zadań można rozwiązywac prosciej, a szczególnie zadań szablonowych np. z ciagów, równania okręgu, funkcji liniowej i kwadratowej, wielomianów itp. Bo wiele zadań jest rozwiązywanych w sposób pogmatwany, np. ciągi rozwiązuje się układami równań, a można na jednej niewiadomej, równanie okręgu metodą "dodać−odjąć" zamiast stosować proste wzory przeliczające współczynniki itp. Mało który nauczyciel pokazuje geometryczną metodę rysowania wykresu funkcji liniowej, niemal wszyscy robą tabelkę i liczą punkty, podobnie jest z polem trójkąta w układzie współrzędnych − zamiast prostym i łatwym do zapamiętania wzorem z wyznacznika wektorów kombinuje się poprzez liczenie podstawy i wysokości. Schemat Hornera to naprawdę rzadkość w szkołach, a jest o wiele szybszy niż dzielenie wielomiaów czy grupowanie tam, gdzie współczynniki nie pasują do siebie i trzeba się nieźle nakombinować, jak je porozbijać, aby pasowały. I o to i przede wszystkim chodzi − o wskazanie prostych i szybkich metod, bo na maturze NIE MA CZASU na metody dookoła swiata. Pozdrawiam

Eta: