1/ wzór na pole; P= a*b/2 a,b, --- przyprostokatne
drugi wzór P= p*r r=2cm p --- połowa obwodu Δ-ta
z tw. Pitagorasa c2 = a2 +b2
znasz a= 6cm
więc; (**) P=3*b i (***) P= 2*p to 3b= 2p
Potrzebne jeste obliczenie długości "b"
więc: Ob= 2p= a+b +c czyli 3b= 6 +b +c
czyli 2b= 6+c to c= 2b -a skoro a= 6cm
to c= 2b - 6
wstawiamy tę wartość do równania c2= a2 +b2
(2b -6)2 = 36 +b2
4b2 - 24b +36 = 36 +b2
to 3b2 - 24b =0 /: 3
b2 - 8b=0 to b(b-8)=0 to b= 0 --- odrzucamy bo b >0
pozostaje b= 8 cm
czyli pole trójkąta jest;
P= a*b/2 czyli P= 6*8/2= 24 cm2
to wszystko!
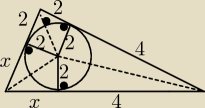(x+4)2=(x+2)2 + 62
x2+8x+16=x2+4x+4+36
4x=24/ :4
x=6
mamy przyprostokątne: 8 i 6
| 8*6 | 48 | |||
P= | = | =24cm2 | ||
| 2 | 2 |
