Kyd: Dla jakich wartości paraaetru p (p e R) miejsca zerowe xq,x2, funkcji kwafratowej f(x)=2x² +(p+3)x+2(p+1)² spełniają warunek x1x2(x1+x2)<0 ? No i tak: wyliczyłem z f(x) delte : Δ= kolejnej delcie. No więc miejsca zerowe wyszły : p1=−1,4

	1
p2=−
	3

Co z tym dalej? Ja podstawiłem do f(x) raz jedno miejsce zerowe za p, a drugi raz drugie miejsce zerowe za p. Znowu delta i raz wszyło

	2
x1=−
	5

a za drugim razem

	2
x1=−
	3

Po jednym miejscu zerowym I teraz coś trzeba by zrobić dalej ale nie wiem co. Czy w ogóle dobrze robiłem? A może źle? Od jakiego momentu? Proszę o pomoc

Kyd:

Godzio: f(x) = 2x² + (p + 3)x + 2(p + 1)² Δ = (p + 3)² − 16(p + 1)² = (p + 3 − 4(p + 1))(p + 3 + 4(p + 1)) = = (p + 3 − 4p − 4)(p + 3 + 4p + 4) = (−3p − 1)(5p + 7) > 0

	1
p1 = −
	3

	7
p2 = −
	5

	7		1
p ∊ (−		,−		)
	5		3

x₁x₂ * (x₁ + x₂) < 0

−(p + 3)		2(p + 1)2
	*		< 0
2		2

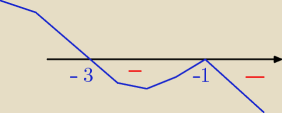
−(p + 3)(p + 1)² < 0 p = −3 lub p = −1 p ∊ (−3,−1) ∪ (−1,∞) Biorąc pod uwagę p z delty otrzymujemy rozwiązanie:

	7		1
p ∊ (−		,−1)∪(−1,−		)
	5		3

Kyd: Godzio, a dlaczego tam jak masz

−(p+3)		(p+1)2
	*		to zniknęły Ci mianowniki? jeden skróciłeś z dwójką, a co się stało
2		2

z drugim?

Bog: pomnozyl obustronnie razy 2, a 0 razy 2=0