Twierdzenie cosinusów PILNE!!!!!!!!!!!!!: W trójkącie ABC dwa boki mają długość 3 i 5 a środkowa poprowadzona do trzeciego boku ma długość 4. Oblicz pole tego trójkąta.

terminex: pomagam

PILNE!!!!!!!!!!!!!: to czekam na pomoc

tadek: srodkowa dzieli trojkat na 2 rowne pola. z wzoru herona nalezy policzyc P1 malego trojkata i P2 malego trojkata a nastepnie porownac je co pozwoli wyeliminowac niewiadoma c i obliczyc P

PILNE!!!!!!!!!!!!!: ale czy to bedzie zgodne z twierdzeniem cosinusow

tadek: a musisz je tu wykorzystywac?

PILNE!!!!!!!!!!!!!: tak tak

tadek: pomysle

PILNE!!!!!!!!!!!!!: no dobrze ja mam wzor zapisany ale zadania nie umiem zrobic

ceaser I: do twierdzenia przydałby sie jakiś kąt

PILNE!!!!!!!!!!!!!: no tak ale podobno mozna rozwiazac bez kata

ceaser I: podyktowała wam takie zadanie czy to jest z ksiązki ?

PILNE!!!!!!!!!!!!!: z ksiazki ale zostalo podyktowane na lekcji

a: Piszesz dwa układy równań, korzystając z twierdzenia cosinusów, dla trójkąta pierwotnego i trójkąta utworzonego na skutek poprowadzenia środkowej.

ceaser I: nazwijmy połowę nieznanego boku c wiec układ c=3²+4²−2*3*4*cos γ c=5²+4²−2*4*5*cos γ

ceaser I: c² oczywiście

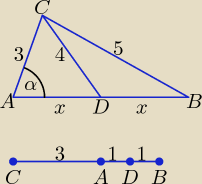
Bogdan: Założenie: x > 0 Na podstawie twierdzenia cosinusów: 16 = 9 + x² − 6xcosα ⇒ 7 = x² − 6xcosα 25 = 9 + 4x² − 12xcosα ⇒ 16 = 4x² − 12xcosα ⇒ 4 = x² − 3xcosα

	1
Odejmując równania stronami otrzymujemy: 3 = −3xcosα ⇒ cosα = −
	x

	1
7 = x2 + 6x *		⇒ x2 = 1 ⇒ x = 1 lub x = −1 sprzeczność
	x

	1
cosα = −		= −1 ⇒ α = 180o
	1

Punkty A, B, C są współliniowe, można powiedzieć, że trójkąt ABC ma pole równe 0.