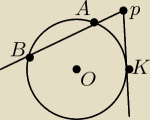
z punktu P, którego odległość od środka O... poziomka: Treść: z punktu P, którego odległość od środka O okręgu jest równa 5cm, poprowadzono styczną do okręgu w punkcje K oraz sieczną przechodzącą przez okrąg w punktach A i B. Wiedząc, że promień okręgu ma długość 3cm i |BP| : |AP| = 3:2, oblicz długość odcinka AB. Jedyne, co mi przychodzi, to twierdzenie o odcinkach sieczne i stycznej, co by wyglądało: |PB| * |PA| = |PK|² czyli 9x² * 4x² = |PK|² ale mógłby ktoś podpowiedzieć, co dalej?.

poziomka: odświeżam, może znajdzie się ktoś kto pomoże

mary: Trójkąt ABO jest równoramienny, jego bok AB=3x, wysokość Od dzieli go na dwie równe części więc odcinek DA=3/2x Z twierdzenia Pitagorasa dla trójkąta ODA h do kwadratu + (3/2x) do kwadratu = 3 do kwadratu Dla trójkąta ODP h do kwadratu + (7/2x) do kwadratu = 5 do kwadratu Po rozwiązaniu tego układu x= 2pierwiastki z 10 /5 AB = 6 pierwiastków z 10/5

mary: x=2√10/5 AB=6√10/5

cezpiw: mary wydaje mi się, że twoje rozwiązanie jest złe, poziomka zaczęła dobrze. możesz obliczyć |PK|: z danych masz |OP|=5, a skoro PK jest styczną, to masz kąt prosty PKO, teraz jedziesz już Pitagorasem (OK to promień) i podstawiasz długość PK pod swój wzorem z twierdzenia o siecznej i stycznej

rafal: złe założenie jest To docinek AP= 2x a AB jest równy x zeby stosunek był dobry bo ma być BP;AP przy poim oznaczeniu jest wtedy dobrze odcinek PK obliczymy ze jest =4 z Pitagorasa długości OP i promienia i stosujemy twierdzenie nieco przekształcone ze BP*AP=PK² wstawiamy i obliczamy i koniec zadania odp to 2√6 przez 2