| 3(a+b+c) | ||
1. Udowodnij, że w dowolnym trójkącie zachodzą nierówności: | <sa+sb+sc<a+b+c | |
| 4 |
 i dziękuje za wszelaką pomoc.
i dziękuje za wszelaką pomoc.
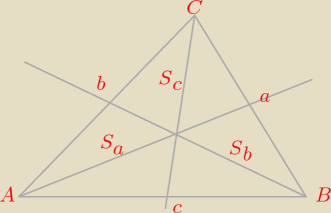 1. Środkowe w trójkącie dzielą się w stosunku 2 : 1, z nierówności w trójkącie mamy:
1. Środkowe w trójkącie dzielą się w stosunku 2 : 1, z nierówności w trójkącie mamy:
| 2 | 2 | ||
sc + | sb > a | ||
| 3 | 3 |
| 2 | 2 | ||
sa + | sb > c | ||
| 3 | 3 |
| 2 | 2 | ||
sa + | sc > b + | ||
| 3 | 3 |
| 4 | 4 | 4 | |||
sa + | sb + | sc > a + b + c | |||
| 3 | 3 | 3 |
| 3 | |
(a + b + c) < sa + sb + sc | |
| 4 |
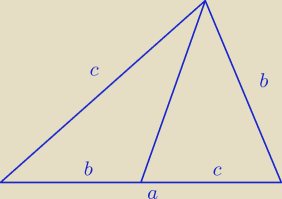 Żeby z trójkąta powstały 2 trójkąty prosta musi przechodzić prze jeden z wierzchołków i
przechodzić przez przeciwległy bok, załóżmy że tak jest, aby trójkąty były przystające
odpowiednie boki muszą być sobie równe, nigdy tak jednak nie będzie, gdyż suma boków musiała
by się równać trzeciemu bokowi:
b + c = a lub b = c (gdy a zostanie podzielone na pół) −− co do pierwszej równości, nigdy nie
zajdzie bo przy takich długościach nie powstanie trójkąt, druga także odpada bo jest to
trójkąt różnoboczny,
Mam nadzieję że takie uzasadnienie wystarczy
Żeby z trójkąta powstały 2 trójkąty prosta musi przechodzić prze jeden z wierzchołków i
przechodzić przez przeciwległy bok, załóżmy że tak jest, aby trójkąty były przystające
odpowiednie boki muszą być sobie równe, nigdy tak jednak nie będzie, gdyż suma boków musiała
by się równać trzeciemu bokowi:
b + c = a lub b = c (gdy a zostanie podzielone na pół) −− co do pierwszej równości, nigdy nie
zajdzie bo przy takich długościach nie powstanie trójkąt, druga także odpada bo jest to
trójkąt różnoboczny,
Mam nadzieję że takie uzasadnienie wystarczy 