Kamil: W trapez równoramienny o przekątnej długości 13c można wpisać okrąg. Odcinek łąćzącuy środki
trapezu ma długość 12c. Oblicz długość ramienia i pole tego trapezu.
10 sty 20:42
Kamil:

|EF|=12
|AC|=13
a+b=c+d
a+b=c+d =>26=c+d => c=13, d=13 (bo trapez równoramienny)
No i nie wiem czemu, ale wg odpowiedzi ramię jest równe 12.
A jak wyznaczyć wysokość?
10 sty 20:49
Kamil: halo?
10 sty 20:58
Eta:
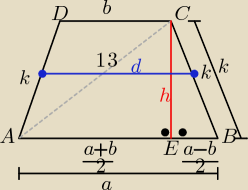
Z warunku wpisania okręgu w ten trapez:
| | a+b | |
linia środkowa trapezu : d= |
| = 12 cm
|
| | 2 | |
co oznacza ,że
k= 12 cm
z Δ AEC z tw. Pitagorasa: h
2= 13
2 − 12
2 = 25 => h= 5 cm
| | a+b | |
P(trapezu)= |
| *h= 12*5= 60 cm2
|
| | 2 | |

10 sty 21:06
Kamil: Ale dlaczego nie robisz tego ze wzoru? Mieliśmy podany taki :
x− środkowa łącząca dwa ramiona
a− podstawa
b− podstawa
10 sty 21:09
Eta:
No przecież to, to samo

Ja oznaczyłam środkową przez "d"
10 sty 21:16
Kamil: Do dobra, ja nie umiem nawet podstawić dobrze

10 sty 21:27
Kamil: A skąd wiadomo, że |AE| = d?
10 sty 21:51
kiks: O to samo pragnę spytać, przeglądam już kolejne rozwiązanie i wszędzie jest stosowany ten
warunek, niestety nie mam zielonego pojęcia skąd to się bierze.
20 kwi 18:30
E30Tomas:
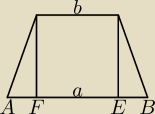
Podzielcie sobie podstawę na 4 części.
odcinek |AF| =
a−b2
odcinek |FE| = b
Czyli odcinek |AE| = |AF| + |FE| =
a−b2 + b =
a−b+2b2 =
a+b2
21 kwi 21:36
 |EF|=12
|AC|=13
a+b=c+d
|EF|=12
|AC|=13
a+b=c+d
 Z warunku wpisania okręgu w ten trapez:
Z warunku wpisania okręgu w ten trapez:

 Ja oznaczyłam środkową przez "d"
Ja oznaczyłam środkową przez "d"

 Podzielcie sobie podstawę na 4 części.
odcinek |AF| = a−b2
odcinek |FE| = b
Czyli odcinek |AE| = |AF| + |FE| = a−b2 + b = a−b+2b2 = a+b2
Podzielcie sobie podstawę na 4 części.
odcinek |AF| = a−b2
odcinek |FE| = b
Czyli odcinek |AE| = |AF| + |FE| = a−b2 + b = a−b+2b2 = a+b2