zadania z pomorskiego konkursu matematycznego dzisiaj

zadania z pomorskiego konkursu matematycznego dzisiaj pomozecie to rozwiazac: 1.Wyznacz liczby naturalne A,B,C tak aby 22/5= A + 1/ (B+1/C) 2.Tg kąta ostrego alfa jest równy p. Wykaż, że (cos α)⁻⁴ = p⁴ + 2p² +1 3.Oblicz pole trójkąta prostokątnego wiedząc, że wysokość dzieli przeciwprostokątna na odcinki długości 4+√7 i 4− √7

10 sty 19:16

Bogdan: Zadanie 1.

22

1

C

 = A + 

*

5

 1 
B + 
 C 

C

	2		C
4 +		= A +
	5		BC + 1

A = 4, C = 2, BC + 1 = 5 ⇒ 2B = 4 ⇒ B = 2

10 sty 22:21

Bogdan: Zadanie 2.

	π
tgα = p α ≠		+ k*π, k∊C
	2

sinα		sin²		1 − cos²α
	= p / ² ⇒		= p² ⇔		= p²
cosα		cos²		cos²α

1
	− 1 = p², itd.
cos²α

10 sty 22:31

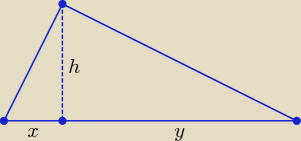
Bogdan: rysunek

Zadanie 3. Trzeba tu skorzystać z zależności: h² = xy

	1
Pole P =		(x + y)*h
	2

10 sty 22:34

.: a czemu h²=xy?

11 sty 16:40