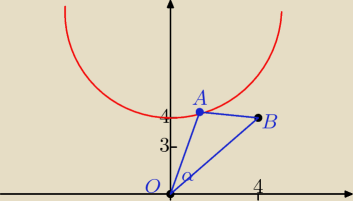
Matura rozszerzona raff: Na wykresie funkcji y=2x² +3 znajdz taki punkt A aby pole trojkata o wierzcholkach A, O=(0,0) i B=(4,4) bylo najmniejsze. wyznacz to pole. Moglibyście też przykładowy rysunek narysować?

Basia: A(x, 2x²+3)

	1
P =		|OA→|*|OB→|*sinα
	2

trzeba to tak przekształcić, aby dostać funkcję zmiennej x

raff:

	1
P =		* |AB| * |AO|
	2

	1
P =		* √(x − 4)2 + ((2x2 + 3) − 4)2 * √(0 − x)2 + (0 − (2x2 + 3))2
	2

Tak może być?

raff: ...

Basia: oczywiście też może, ale ta funkcja będzie o wiele bardziej skomplikowana pierwiastki chyba się nie uproszczą i trzeba będzie zbadać nie P(x) ale P²(x) uzasadniając, że tak można (bo można) natomiast w mojej wystarczy policzyć współrzędne OA^→=[a₁,a₂] i OB^→[b₁,b₂]

	|a1*b2−a2*b1|
sinα =
	|OA→|*|OB→|

co po podstawieniu da

	1
P(x) =		|a1*b2−a2*b1|
	2

to powinno być znacznie prostsze

Basia: oj nie raff, nie można, przecież tam nie musi być kąt prosty