Prawdopodobieństwo Godzio: Jak udowodnić takie coś:

	1		1		1
A,B∊Ω oraz P(A) =		, P(B) =		to		≤ P(A∪B)
	4		3		3

Godzio: A,B⊂Ω miało być

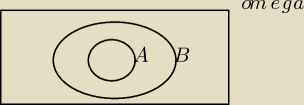
Trivial: Mamy sumę prawdopodobieństw. Najmniejszą możliwą wartością tej sumy jest największy element. Nie wiem jak to ładnie powiedzieć. Ale widać na rysunku. Zakładamy sytuację najbardziej krytyczną, taką, że te elementy z A w całości zawierają się w B.

Godzio: No właśnie chodziło by mi o takie słowne

Trivial: A nie ma jakichś wzorów na P(A u B)? Bo nie pamiętam.

Godzio: A zresztą, rysunek trzasnę i opiszę jakoś swoimi słowami Dzięki

Godzio: P(A∪B) = P(A) + P(B) − P(A∩B)

Trivial: No to pasuje. iloczyn będzie co najwyżej 1/4, czyli: P(A u B) ≥ 1/4 + 1/3 − 1/4 P(A u B) ≥ 1/3

Basia: P(A∪B) ≥ P(A) i P(A∪B) ≥ P(B) dowód: A∪B = (A−B)∪B P(A∪B) = P[(A−B)∪B] = P(A−B)+P(B) − P[(A−B)∩B] = P(A−B)+P(B)−P(∅) = P(A−B)+P(B) ≥ 0+P(B)=P(B) analogicznie pokazujesz, że P(A∪B)≥P(A)

Basia: A wcale nie musi pociągać za sobą B innymi słowy, nie taki rysunek Trivial

Trivial: No tak, wiem. Ale tam jest dopisek, że jest to sytuacja 'krytyczna'.

Noah: Godzio jak dalje jest ci to potrzebne to ci przepisze przyklad z podrecznika jak oni to robia ale podobnie do Basi

Basia: dowód masz wyżej, z niego wynika co trzeba nic o żadnej sytuacji krytycznej tam nie widzę

Godzio: Dzięki Basia Wszystko rozumiem

Trivial: "Zakładamy sytuację najbardziej krytyczną, taką, że te elementy z A w całości zawierają się w B."

Godzio: Noah już nie trzeba

Trivial: To i tak teraz bez różnicy, bo mamy lepszy dowód, a nie wersję na oko.

Basia: Trivial to Ty napisałeś; Godzia zadanie na takie założenie nie pozwala

Trivial: Dalej nie wiem dlaczego nie można zrobić tak jak ja. Jeżeli A nie mieści się całkowicie w B, to prawdopodobieństwo sumy A i B wychodzi większe niż 1/3. ;s W sytuacji krytycznej wychodzi 1/3.

Basia: bo to właśnie trzeba udowodnić

Trivial: Nasz nauczyciel matematyki tak właśnie nam to pokazywał, zanim przeszedł do dowodu na wzorach. Ale już daję spokój.

Bogdan:

	3		4
P(A) =		, P(B) =
	12		12

P(A∪B) = P(A) + P(B) − P(A∩B)

	7
Maksymalna wartość P(A∪B) = P(A) + P(B) =		, tu P(A∩B) = 0
	12

	4		3
Minimalna wartość P(A∪B) = P(B) =		, tu P(A∩B) = P(A) =		, A⊂B
	12		12

	4		7
Stąd		≤ P(A∩B) ≤
	12		12

Trivial: Bogdan na tych samych zasadach opierał się mój sposób. Jak się jednak okazało, jest on nielegalny.

Basia: Trivial dopiero później "załapałam" o co Ci tak naprawdę chodzi. Zmyliły mnie trochę te "warunki krytyczne", a może niedokładnie przeczytałam. One zresztą nie są potrzebne. Twoje rozumowanie w formie uogólnionej (czyli bez tych dodatkowych warunków) można przedstawić tak: dla każdych dwóch A,B⊂Ω ∅⊂A∩B⊂A ∧ ∅⊂A∩B⊂B ⇒ P(∅)≤P(A∩B)≤P(A) ∧ P(∅)≤P(A∩B)≤P(B) ⇒ 0≤P(A∩B)≤P(A) ∧ 0≤P(A∩B)≤P(B) ⇒ P(A∪B) = P(A)+P(B)−P(A∩B)≤P(A)+P(B)−0 = P(A)+P(B) i P(A∪B) = P(A)+P(B)−P(A∩B)≥P(A)+P(B)−P(A) = P(B) i P(A∪B) = P(A)+P(B)−P(A∩B)≥P(A)+P(B)−P(B) = P(A) co ostatecznie da się zapisać tak: max[ P(A), P(B) ] ≤ P(A∪B) ≤ P(A)+P(B) i załatwia sprawę "raz na zawsze" bez dodatkowych "co by było gdyby"