znajdz sume długości wysokokośći w trójkącie karolina: znajdź sumę długosci wysokości trójkąta ABC o wierzchołkach A (−1,1) B(4, −7) C (−1, 3)

esta: Ułóż równania y=ax+b prostych (boków) tego trójkąta. Wysokość poprowadzona z wierzchołka C będzie prostą prostopadłą do prostej AB. Zrób tak ze wszystkimi wysokościami. Dzięki temu znajdziesz drugi koniec wszystkich wysokości. Z resztą powinnaś sobie poradzić.

bart: nawet Ci sie tego narysowac nie chce.. A i C leza w jednej lini to jaki problem? rysujesz wykres i liczysz krateczki

karolina: bardziej mnie interesuje na wzorach

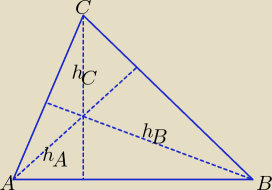
Bogdan: Rysunek pokazuje zastosowane w rozwiązaniu oznaczenia.

	−8		−8
Równanie prostej zawierającej A, B: aAB =		, y =		(x + 1) + 1 / * 5
	5		5

	|−1*8 + 3*5 + 8|		15
8x + 5y + 8 = 0, hC =		=
	√82 + 52		√91

Równanie prostej zawierającej A, C: x = −1

	|4*1 − 7*0 + 1|
x + 1 = 0, hB =		= 5
	√12 + 0

	10
Równanie prostej zawierającej B, C: aBC =		= −2, y = 2(x + 1) + 3
	−5

	|−1*2 + 1*(−1) + 5|		2
2x − y + 5 = 0, hA =		=
	√22 + 12		√5

Zastosowałem w rozwiązaniu wzór na odległość d punktu (x₀, y₀) od prostej Ax + By + C = 0

	|x0*A + y0*B + C|
d =
	√a2 + B2

Zadanie można rozwiązać również innymi sposobami.