ostrosłup k: Mógłby mi ktoś sprawdzić zadanie o następującym poleceniu: Obliczyć h, b i Pc, tak żeby zrobić z tego bryłę wiedząc, że ostrosłup prawidłowy czworokątny ma: a= 9.5 Pb=180.5. Ja zrobiłam to tak: d= a{2} d= 9,5{2} Pb= a*b 180,5=9,5*b b=19 czyli b=h

ICSP: Nie za bardzo czytelnie to polecenie. Z tego co rozumiem to masz ostrosłup prawidływy czworokątny o krawedzi podstawy równej 9,5 oraz powierzchni pocznej równej 180,5?

k: tak, takie mam polecenie

ICSP: a czym jest b?

k: b to wysokosc

ICSP: b− wysokość (zakładam że siany bocznej) h− wysokość ostrosłupa?

k: tak, a ja błędnie przyjęłam sobie, że wysokość ściany bocznej jest tym samym co ostrosłupa,

k: a czy byłaby taka możliwość, żebyś mi napisał/a poprawne rozwiązanie tego zadania?

ICSP: już patrze.

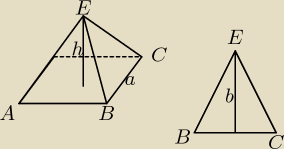
ICSP: D jest czwartym wierzchołkiem podstawy. Powierzchnia boczna składa się z 4 identycznych trojkatow BCE wiec pole jednego takiego

	pb
trojkata bedzie rowne		. Z danych w zadaniu wiemy ze |BC| = a = 9,5.
	4

ICSP:

	1
Pole trójkąta wyraża się wzorem		a*b.
	2

	180,5
Najpierw obliczmy pole trojkąta BCE:		= 45,125
	4

Z tresci wiemy ze a = 9,5

	1
45,125 =		* 9,5 * b ⇔ 90,25 = 9,5b ⇔ b = 90,259,5 ⇔ b =9,5
	2

ICSP: Na koniec twierdzenie pitagorasa: (¹₂a)² + b² = h²

k: Dziękuję Ci bardzo.