 Proszę o pomoc z zadaniem z matematyki z działu Wektory.
Treść zadania:
Znajdź długość wektora MP + KQ, wiedząc, że punkty K, L, M, N są środkami kolejnych boków
jednostkowego kwadratu ABCD, a P oraz Q są punktami przecięcia odpowiednio odcinków NC z ML
oraz NB z KL.
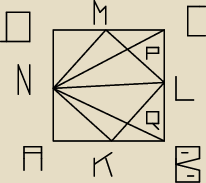
Dodałem rysunek pomocniczy (tak wiem koszmarny).
Dodatkowe informacje:
Czworokąt KLMN − jest kwadratem.
Trójkąty NPL oraz CPM są podobne.
∡NPL=∡CPM są to kąty wierzchołkowe.
∡CPM = 45*(stopni) = ∡PLN
Osobiście, jak obliczałem to zrobiłem tak:
KQ = MP
Proszę o pomoc z zadaniem z matematyki z działu Wektory.
Treść zadania:
Znajdź długość wektora MP + KQ, wiedząc, że punkty K, L, M, N są środkami kolejnych boków
jednostkowego kwadratu ABCD, a P oraz Q są punktami przecięcia odpowiednio odcinków NC z ML
oraz NB z KL.
Dodałem rysunek pomocniczy (tak wiem koszmarny).
Dodatkowe informacje:
Czworokąt KLMN − jest kwadratem.
Trójkąty NPL oraz CPM są podobne.
∡NPL=∡CPM są to kąty wierzchołkowe.
∡CPM = 45*(stopni) = ∡PLN
Osobiście, jak obliczałem to zrobiłem tak:
KQ = MP
| 1 | ||
MP = | ML | |
| 3 |
| 1 | ||
ML = | NL | |
| 2 |
| 1 | ||
MP = | NL | |
| 6 |
| 1 | 1 | |||
KQ + MP= | + | |||
| 3 | 3 |
| 2 | ||
KQ + MP = | ||
| 6 |
| 1 | ||
KQ + MP = | ||
| 3 |