| α | ||
V=2a3sin | √sinα2sin3α2 | |
| 2 |

 prosze
prosze
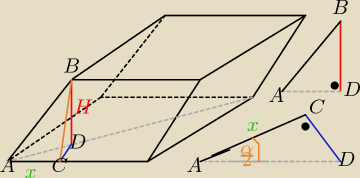 V= Pp*H Pp= a2*sinα
z ΔACB
|AC|= x= a*cosα
wysokość równoległościanu H= |BD| hb= |BC|=a*sinα
z Δprostokatnego ADC , gdzie |< DAC|= α2
i o przeciwprostokątnej AD mamy:
V= Pp*H Pp= a2*sinα
z ΔACB
|AC|= x= a*cosα
wysokość równoległościanu H= |BD| hb= |BC|=a*sinα
z Δprostokatnego ADC , gdzie |< DAC|= α2
i o przeciwprostokątnej AD mamy:
| x | |
= cosα2
| |
| |AD| |
| x | a*cosα | |||
|AD|= | = | |||
| cosα2 | cosα2 |
| a2cos2α | ||
H2= a2− IAD|2 = a2 − | ||
| cos2α2 |
| a | ||
H= | *√ cos2α2− cos2α
| |
| cosα2 |
| a3*sinα | ||
V= | *√cos2α2 − cos2α
| |
| cosα2 |
| a3 *2sinα2*cosα2 | ||
V= | *√cos2α2− cos2α
| |
| cosα2 |
 a więc tak:
cos2α2 − cos2α= 1 − sin2α2 − ( 1−2sin2α2)2=
= 1 − sin2α2 −1 +4sin2α2− 4sin4α2=
= 3sin2α2− 4 sin4α2= sinα2( 3sinα2 − 4sin3α2)
ponieważ ze wzoru : sin 3β= 3sinβ− 4sin3β
to dalej mamy:
= sinα2 * sin3α2
i gotowe
a więc tak:
cos2α2 − cos2α= 1 − sin2α2 − ( 1−2sin2α2)2=
= 1 − sin2α2 −1 +4sin2α2− 4sin4α2=
= 3sin2α2− 4 sin4α2= sinα2( 3sinα2 − 4sin3α2)
ponieważ ze wzoru : sin 3β= 3sinβ− 4sin3β
to dalej mamy:
= sinα2 * sin3α2
i gotowe  V= 2a3*sinα2*√ sinα2*sin3α2 [j3] ....... i gra
V= 2a3*sinα2*√ sinα2*sin3α2 [j3] ....... i gra  P.S. sorry za koślawe rysunki , ale już ledwie na oczy widzę
P.S. sorry za koślawe rysunki , ale już ledwie na oczy widzę
 Pozdrawiam Bogdanie
Pozdrawiam Bogdanie  Powiedz mi przynajmniej, czy jest jakiś prostszy sposób rozwiazania tego zadania?
Powiedz mi przynajmniej, czy jest jakiś prostszy sposób rozwiazania tego zadania?
 Dzień dobry wszystkim. Witaj Eto
Dzień dobry wszystkim. Witaj Eto  , przepraszam, że wczoraj wieczorem nie odpowiedziałem
Ci od razu, zapatrzyłem się transmisję Wielkiej Orkiestry Owsiaka.
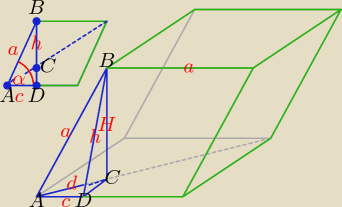
Wielościan którego wszystkie ściany są rombami nazywa się romboedr. Mając daną miarę
kąta ostrego rombu α i długość jego boku a obliczyłbym objętość tej bryły w ten sam sposób.
, przepraszam, że wczoraj wieczorem nie odpowiedziałem
Ci od razu, zapatrzyłem się transmisję Wielkiej Orkiestry Owsiaka.
Wielościan którego wszystkie ściany są rombami nazywa się romboedr. Mając daną miarę
kąta ostrego rombu α i długość jego boku a obliczyłbym objętość tej bryły w ten sam sposób.
| α | c | ||||||||||||
|AC| = d, |AD| = c, |∡CAD| = | , c = acosα, d = | ||||||||||||
| 2 |
|
| a | ||
H = √a2 − d2 = | √ cos2α2 − cos2α | |
| cosα2 |
| a | ||
V = a2sinα * H = a2 * 2sinα2cosα2 * | √ cos2α2 − cos2α = | |
| cosα2 |
| 32α | α2 | 32α | α2 | |||||
= 2sin | sin | * 2cos | cos | = | ||||
| 2 | 2 | 2 | 2 |
| 3 | α | |||
= sin | α * sin | |||
| 2 | 2 |