stereometria? a: Trójkąt ABC jest podstawą ostrosłupa prawidłowego ABCW o wysokości 4 i objętości √3/3. Punkt C1 jest rzutem prostokątnym punktu C na przeciwległą ścianę ostrosłupa, a BB1 to wysokość ściany ABW to tak, zabrałem się za to sam i wyszło mi tak: boki trójkąta(podstawy) wynoszą a=1 każdy wysokość pada pod kątem prostym na punkt przecięcia się wysokości trójkąta równobocznego, więc żeby obliczyć wysokość ściany ABW wystarczy, że obliczę 1/3 wysokości trójkąta h=^√3₂ więc 1/3 h = ^√3₆ H − wysokość ściany ABW H² = 4² + (^√3₆)² H²=16+³₃₆ H²=^{36*16 +1}₃₆=⁵⁷⁹₃₆ H= ^√579 ₆ Dobrze obliczyłem wysokość tej ściany ABW? Bo potem jeszcze trzeba obliczyć pole trójkąta BB₁C₁ ale na razie nie wiem czy dotąd dobrze robie.

a: pole trójkąta BB₁C₁ wyszło mi P= ^√3 ₁₆ ale wydaje mi, się że z czymś pochrzaniłem... pewnie z tymi rzutami... Proszę o pomoc

a: nikt nie pomoże?

a: odświeżam

Trivial: Zaraz spróbuję.

Trivial: Zadanie praktycznie rozwiązane. Zjem obiad to napiszę.

a: No właśnie zależy mi na sprawdzeniu, bo wydaje mi się że coś pokręciłem i jest źle, ale sam już nie wiem..

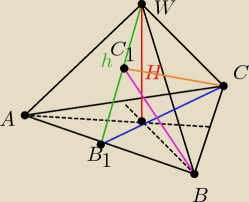
Trivial: Czy to dobry rysunek?

a: problem w tym, że sam nie wiem, mi wyszedł inny... bo B1 dałem naprzeciwko B, czyli na końcu wysokości poprowadzonej od punktu B do boku AC, C1 podobnie...

Trivial: Chodzi mi o: "...BB1 to wysokość ściany ABW..."

a: Nie wiem czemu dałeś B₁ tam gdzie dałeś... i C₁ też... to jest ten rzut prostokątny?

a: a no ok

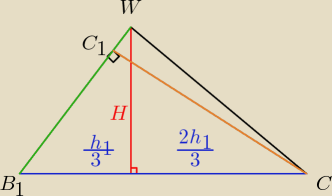
Trivial: h₁ to wysokość podstawy ostrosłupa. Czy dalej dasz sobie radę?