geometria Agu: Bardzo proszę o pomoc, jedno z zadań maturalnych którego nie umiem rozgryźć, Punkt E leży na ramieniu BC trapezu ABCD, w którym AB∥CD. Udowodnij, że |∡AED|=|∡BEA|+|∡CDE|. Proszę o pomoc : /

Marcin W: tresc jest na pewno ok ?

Agu: ∡|BAE| ma być zamiast BEA, literki przestawiłam, przepraszam : X

Marcin W: no wlasnie cos mi nie gralo

Agu: Mi całe te zadanie nie gra, więc wiesz

Marcin W: no tak ale jak jest zla tresc to wybacz ze Cos udowodnie poza tym ze tresc jest zla

Agu: No tak . Ale teraz gdy treść jest poprawiona, to pomożesz?

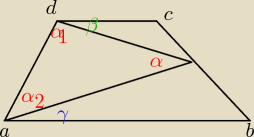
Marcin W: z rysunku mamy: α₂+γ+α₁+β=180 czyli *** α₁+α₂+γ+β=180 ale α₁+α₂+α=180⇒ α₁+α₂=180−α podstawiajac to do ** mamy: 180−α+γ+β=180 α=γ+β

Marcin W: tam gdzie wierzcholek kata α na rysunku powinien być punkt E.

Agu: a po co ***?

Marcin W: zeby pozniej napisac "podstawiajac do ***" chodzi o to zebys wiedziala gdzie to podstawiłem równie dobrze moglem oznaczyć to jako równanie a) albo cokolwiek innego zby potem napisac podstawiając do a) rozumiesz ? Chodzi o cos takiego np x+5x²=2 oznaczam to sobie przez * pozniej moge uzyc zapisu podstawiajac za x=8 do * czyli do tego równania ktore tak oznaczylem...

Agu: Ach, rozumiem . Zadanie w sumie wydaję się trudne, ale jak to rozpisałeś, to łatwe jest : O Dziękuje Ci bardzo

Marcin W: pozdrawiam