mmm
aga: W pierwszej urnie znajdują się 4 kule białe i 6 niebieskich, w drugiej− 3 białe, 5 żółtych i 2
niebieskie. Rzucamy monetą: jeśli wypadnie orzeł to− losujemy kulę z pierwszej urny, jeśli
reszka− z drugiej. Jakie jest prawdopodobieństwo wylosowania kuli:
a) białej
b) żółtej
c) niebieskiej?
7 sty 15:55
Marcin W: drzewkiem latwo bedze

7 sty 15:58
aga: ale jak

?
7 sty 16:00
Marcin W: Jednak niekoniecznie
B− wylosowano białą kulę
7 sty 16:00
7 sty 16:01
aga: skad to wzieles?
7 sty 16:02
Marcin W: sory zle
7 sty 16:03
Marcin W: już ci rysuje drzewko

zaczekaj
7 sty 16:04
aga: oki dzieki

7 sty 16:05
Marcin W:
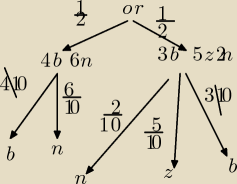
7 sty 16:09
Marcin W: | | 1 | |
na gorze drzewa mamy po |
| bo prawdopodobienstwo zarówno orła jak i reszki (wyrzucenia) |
| | 2 | |
| | 1 | |
jest równe własnie |
| potem na poszczególnych galęziach masz poszczególne |
| | 2 | |
prawdopodobienstwa losujesz jedna kule z urny wiec latwo policzyc ile wynosi
prawdopodobienstwo wylosowania danej kuli z danej urny. Dalej wszystkie odp podasz z drzewka.
7 sty 16:11
Marcin W: Więc dasz sobie teraz radę ?
7 sty 16:11
aga: nie bardzo

7 sty 16:12
Marcin W: | | 1 | | 4 | | 1 | | 3 | | 7 | |
a) P(A)= |
| * |
| + |
| * |
| = |
| bo tak trzeba "isc" od "wierzcholka" drzewka |
| | 2 | | 10 | | 2 | | 10 | | 10 | |
aby dojsc do kuli b (czytaj bialej)
| | 1 | | 6 | | 1 | | 2 | | 2 | |
c)P(N)= |
| * |
| + |
| * |
| = |
| |
| | 2 | | 10 | | 2 | | 10 | | 5 | |
7 sty 16:16
aga: i to juz koniec?
7 sty 16:19

 ?
?
 zaczekaj
zaczekaj


