Oblicz pole czworokata wypukłego ABCD, w którym katy wewnetrzne maja odpowiednio elunia1521: Oblicz pole czworokata wypukłego ABCD, w którym katy wewnetrzne maja odpowiednio miary: A = 90o, B = 75o, C = 60o, D = 135o, a boki AB i AD maja długosc 3cm

elunia1521:

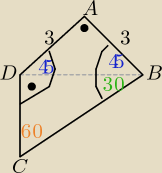
Eta: Rysunek wszystko wyjaśnia otrzymasz podział na dwa trójkąty prostokątne |<ADC|= 135^o , |<ADB|= |<ABD|= 45^o to |<CDB|= 135^o −45^o=90^o ΔABD −− jest prostokątny i równoramienny o ramionach: |AD|= |AB|= 3 to |BD|= 3√2 ΔCBD −− jest też prostokątny, bo |<CDB|= 90^o i |<DCB|= 60^o zatem : |DC|= √6 , |CB|= 2√6

	1		1
P(ABCD)=		3*3 +		*3√2*√6= ....... dokończ obliczenia
	2		2

elunia1521: Oblicz pole czworokata wypukłego ABCD, w którym katy wewnetrzne maja odpowiednio miary: A = 90o, B = 75o, C = 60o, D = 135o, a boki AB i AD maja długosc 3cm

Eta: elunia ....... o co Ci jeszcze chodzi Nie umiesz wykonać prostych działań ?

	9		3√12		3√4*3		3*2√3
P(ABCD) =		+		=4,5+		= 4,5+		= 4,5+ 3√3
	2		2		2		2