układ współrzędnych zarus333: witam, prosiłbym o rozw. szczegółowe bo juz sobie z tym nie radze... z góry dzieki Zad. Wierzchołki trójkąta mają współrzędne A=(4,0), B=(−4,4), C=(−5,−3) a) znajdź równanie prostej przechodzącej przez punkt C i zawierającej wysokość tego trójkąta b) oblicz pole trójkąta ABC

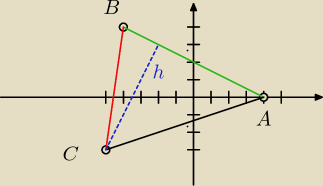
dero2005: Szukamy równania prostej boku AB (zielony) (−4−4)(y−0) = (4−0)(x−4) y = −¹₂x+2 Szukamy prostej prostopadłej do boku AB i przechodzącej przez punkt C (niebieski) warunek prostopadlości a₁*a₂ = −1 a₁ = −¹₂ a₂ = 2 y = a₂(x−x_C)+y_C y = 2(x+5)−3 y = 2x + 7 Liczymy długość odcinka |AB| d = √(x_A−x_B)² +( y_A−y_B)² d = √(4+4)² + (0−4)² = 4√5 Liczymy długość wysokości (niebieski) jako odleglość punktu C od prostej (zielonej)

	|Axo + Byo + C|
d =
	√A2+B2

	|−12*(−5) + (−1)*(−3) + 2|
d =		= 3√5
	√(−12)2 + (−1)2

Pole trójkąta

	|AB|*h		4√5*3√5
P =		=		= 30
	2		2