
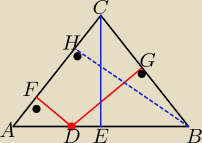
 może z podobieństwa trójkątów coś wyniknie
jest ich tu całe stado
tr.AFD~tr.AEC~tr.AHB~tr.BGD~tr.BEC
może z podobieństwa trójkątów coś wyniknie
jest ich tu całe stado
tr.AFD~tr.AEC~tr.AHB~tr.BGD~tr.BEC
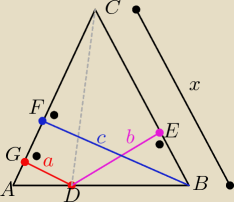 Wprowadzam oznaczenia:
IAC|= |BC| = x , x >0 IDG|= a |DE|= b |BF|= c
Mamy wykazać,że c= a+b
dowód:
Wprowadzam oznaczenia:
IAC|= |BC| = x , x >0 IDG|= a |DE|= b |BF|= c
Mamy wykazać,że c= a+b
dowód:
| 1 | ||
P(ΔABC)= | x*c
| |
| 2 |
| 1 | 1 | 1 | |||
x*c= | x*a + | x*b .... dzielimy przez 12x
| |||
| 2 | 2 | 2 |
