wektory :): Napisz równanie okręgu o środku w punkcie S=(1;−1) odcinającego na prostej o równianiu x−2y+3=o cięciwę długości 16

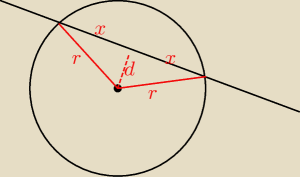
Basia: 2x=16 x=8 d − odległość S(1,−1) od prostej

	|1*1−2*(−1)+3|
d =		=
	√12+(−2)2

|1+2+3|		6
	=
√1+4		√5

z tw.Pitagorasa r²=x²+d²

	36		320+36		356
r2 = 64+		=		=
	5		5		5

	√356
r =
	√5

a=1 b=−1 postaw do wzoru okręgu i tyle

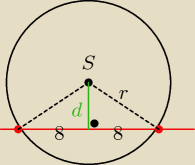Eta: odległość "d" punktu S od cięciwy:

	|1*1−2(−1)+3|		6
d=		=
	√12+22		√5

	36		356
r2= d2 +82 =		+64=
	5		5

	356
o: ( x−1)2 + ( y+1)2=
	5

Eta:

:): dziękuje