POMOCY!!! Areczek 0078: Punkt M jest punktem wewnętrznym czworokąta wypukłego. Udowodnij, że suma odległości punktu M od wierzchołków danego czworokąta jest większa od połowy jego obwodu. POMOCY

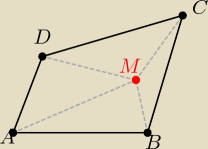
Eta: Ob(ABCD)= IAB| + |BC| + |CD| + |DA| z warunku trójkąta: |AB| > |AM| + |BM| |BC| > ||BM| + |CM| |CD| > |CM| + |DM| |DA| > ||DM| + |AM| −−−−−−−−−−−−− dodając stronami: |AB|+ |BC| + |CD| + |DA| > 2|AM| + 2|BM| + 2|CM| + 2|DM|

	1
|AM| + |BM| + |CM| + |DM| <		(|AB|+ |BC| + |CD| + |DA|)
	2

c. n.u.