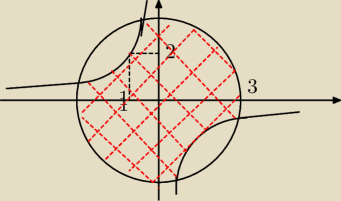
Funkcja homograficzna i okrąg - zapisz układ nierówności. djarek: Zapisz układ nierówności opisujący zamalowany zbiór punktów (łącznie z brzegiem), wiedząc że jest on wyznaczony przez pewną funkcję homograficzną f i okrąg.

Basia: okrąg o środku O(0,0) i promieniu 3 jego równanie to x²+y²=9 f.homograficzna

	a
y=
	x

	a
2=
	−1

a=−2

	−2
y=
	x

stąd: x²+y²≤9 i

	−2
y≤		dla x<0
	x

i

	−2
y≥		dla x>0
	x

djarek: Ok. Ale w ten sposób wykluczamy punkty dla x=0. Powinno być w rozwiązaniu: x²+y²≤9 yx≥−2 Chodzi mi o szerszy problem. Jak zapisać nierówność w przypadku funkcji homograficznej, jeśli chcemy mieć obszar "pomiędzy" gałęziami wykresu lub na "zewnątrz" tych gałęzi. Inaczej mówiąc czy jak zapiszę (w ogólnym przypadku):

	a
(y−b)(x+c)≥a to otrzymam obszar "pomiędzy" gałęziami wykresu funkcji y=b+		oraz
	x+c

	a
(y−b)(x+c)≤a to otrzymam obszar "na zewnątrz" gałęzi wykresu funkcji y=b+		.
	x+c