POMOCY Jola: napisz rownanie symetrycznej odcinka o koncach A=(−2;−3) B=(6;5)

dero2005: znajdź środek odcinka |AB|

	xA+xB		yA+yB
s(xs,ys) = (		;		)
	2		2

znajdź równanie prostej przechodzącej przez punkty A i B (x₂−x₁)(y−y₁)=(y₂−y₁)(x−x₁) znajdź równanie prostej przechodzącej przez punkt S i prostopadłej do prostej AB, będzie to równanie symetralnej odcinka

dero2005: 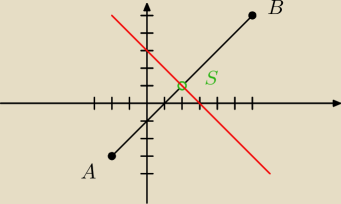S(2,1) y = x−1 y = −x + 3

dero2005: możesz też skorzystać z wzoru uproszczonego (2x−x_A−x_B)(x_A−x_B)+(2y−y_A−y_B)(y_A−y_B)=0 gdzie: x_A =−2 x_B = 6 y_A =−3 y_B = 5

Gustlik: Dero, dlaczego lubisz się męczyć trudnymi, ciężko strawnymi i długimi jak tasiemiec wzorami? Skad wziąłeś ten "uproszczony" a raczej pogmatwany wzór (2x−x_A−x_B)(x_A−x_B)+(2y−y_A−y_B)(y_A−y_B)=0 ? Równania prostych najlepiej wyprowadzać ze wzoru na współczynnik kierunkowy:

	yB−yA
a=		. te długie wzory właśnie się wzięły z tego wzoru na a.
	xB−xA

Jets to wzór ułatwiający, a nawet ratujący życie w wielu przypadkach. Szczerze mówiąc ten długi wzór na równanie prostej przechodzący przez 2 punkty który Ty stosujesz w zasadzie nie jest przydatny do niczego. Napisz rownanie symetrycznej odcinka o koncach A=(−2;−3) B=(6;5) Najprościej tak: 1. Liczę współczynnik kierunkowy prostej AB, na której leży odcinek:

	yB−yA		5−(−3)		8
a1=		=		=		=1
	xB−xA		6−(−2)		8

2. Liczę współrzędne środka odcinka:

	xA+xB		yA+yB		−2+6		−3+5
S=(		.		)=(		,		)=(2, 1)
	2		2		2		2

3. Liczę współczynnik kierunkowy symetralnej z warunku prostopadłości do prostej AB:

	1		1
a2=−		=−		=−1
	a1		1

Symetralna ma równanie: y=−x+b Postawiam współrzędne srodka odcinka: 1=−2+b 1+2=b b=3 Odp: y=−x+3

Trivial: Wzory tasiemce są najlepsze!

Gustlik: Tiaaa. chyba po to, żeby się pogubić i oblać maturę, zeby egzaminatorzy mieli co robić w sierpniu napoprawkach.****