równanie konrad509: Wyznacz liczbę rozwiązań równania a²+||x+1|−1|=1 w zależności od parametru a.

Jack: narysuj sobie f(x)=||x+1|−1|−1 oraz g(x)=−a². poszukaj przecięć f(x) i g(x).

konrad509: A czemu tak? Poza tym chcę obliczeń a nie odczytywania z wykresu.

Godzio : Nie da się z obliczeń dojść do rozwiązania, niestety trzeba narysować

konrad509: No w sumie racja, można to odczytać z wykresu, bo chodzi o ilość rozwiązań a nie jakie one są, bo tego by się nie dało dokładnie odczytać. Ale teraz mi powiedzcie dlaczego to trzeba rozłożyć na te dwie funkcje?

Godzio: No właśnie po to żeby dało się odczytać, jak narysujesz wykres mający 2 zmienne ?

konrad509: Dobra, powiedzmy że rozumiem

konrad509: No dobra, z wykresów wychodzi że są dwa rozwiązania, ale nie wiem dokładnie dla jakiego 'a'. Tak więc co mi to daje?

Godzio: To masz ustalić, zaraz pokażę o co chodzi

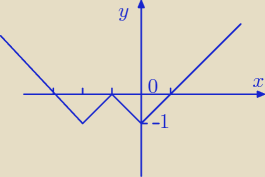
Godzio: Jeśli −a² < −1 −− brak rozwiązań ⇒ a ∊ ... Jeśli −a² = −1 lub −a² > 0 −− 2 rozwiązania ⇒ a ∊ ... Jeśli −1 < −a² < 0 −− 4 rozwiązania ⇒ a ∊ ... Jeśli −a² = 0 −− 3 rozwiązania ⇒ a = 0

konrad509: a∊(−∞,−1)u(1,∞) a∊{−1,1} a∊(−1,0)u(0,1) Dobra, to co zapisałeś pod wykresem rozumiem, ale jak patrze na wykresy i na te przedziały które wyznaczyłem to jakoś ich tam nie widzę Wrócę jeszcze do początku zadania. Czemu rozdzielając to równanie przed a² postawiłeś minus, a ||x+1|−1| zostawiłeś tak jak jest? Nie mogę właśnie też zrozumieć sposobu rozdzielnia.

Godzio: ||x + 1| − 1| + a² = 1 /−a² − 1 ||x + 1| − 1| − 1 = −a² Można to napisać w postaci: −||x + 1| − 1| + 1 = a² tylko wtedy inny wykres będzie

konrad509: Aha, dobra rozumiem. Dzięki