Oblicz długość boków równoległoboku , którego obwód jest równy 66 a stosunek wys Agula: Oblicz długość boków równoległoboku , którego obwód jest równy 66 a stosunek wysokości jest

	4
równy		.
	7

Proszę pomóżcie

Eta: a, b −− długości boków 2a+2b=66 => a+b= 33

h1		4
	=
h2		7

P= a*h₁ i P= b*h₂ a*h₁= b*h₂

	b		h1		4
		=		=
	a		h2		7

rozwiąż układ: a+b= 33

	b		4		4
		=		....... => b=		*a
	a		7		7

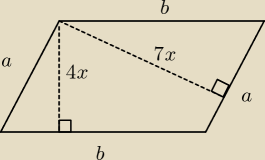
Trivial: L − obwód P − pole równoległoboku L = 2(a + b) = 66 P = a*7x = b*4x → 7a = 4b 2a + 2b = 66 7a = 4b Dalej już wiadomo.

Gustlik: Skorzystam z rysunku Triviala, bo dobrze narysował,a mi rysowanie zawiesza kompa: Nietrudno zauważyć, że trójkąty wyznaczone przez wysokość 7x i bok a oraz wysokość 7x i bok b są podobne, bo działa tutaj cecha kąt−kąt podobieństwa trójkątów (mają one po kącie prostym i dwa naprzeciwległe kąty ostre równoległoboku, które są równe). Zatem a=4y, b=7y, bo stosunek boków a i b musi być taki sam, jak stosunek wysokości. Ponieważ w zadaniu mam podany obwód, policze teraz obwód na "y"−ach i przyrównam do wartości podanej w zadaniu: 2*4y+2*7y=66 /:2 4y+7y=33 11y=33 /:11 y=3 Zatem: a=4*3=12 b=7*3=21 I nie potrzeba układów równan, można obliczyć na jednej niewiadomej.

Gustlik: Mała poprawka − wkradła się literówka: trójkąty wyznaczone przez wysokość 4x i bok a oraz wysokość 7x i bok b są podobne, bo działa tutaj cecha kąt−kąt podobieństwa trójkątów (mają one po kącie prostym i dwa naprzeciwległe kąty ostre równoległoboku, które są równe).

Eta: A cóż to "za układ" ? ( tak tylko go określiłam) Zwykłe "czepiactwo" Gustliku od daaaaaaaaaaawna i chyba tak Ci już pozostanie : "do końca świata i o jeden dzień dłużej"

Gustlik: Eta, ja sie nie czepiam, ale widzę że niektórzy próbują tutaj używać bomby atomowej do zabicia muchy, bo tak ich nauczyli nauczyciele, a wystarczyłaby zwykła łapka. Układy równań z dwiema, a nawet trzema niewiadomymi tam, gdzie wystarczy proste równanko z jedną niewiadoma, wyznaczanie równania prostej przechodzacej przez dwa punkty dłuuuugim jak tasiemiec i "mało strawnym" wzorem, obliczanie naokoło pola trójkąta w układzie współrzędnych, obliczanie układami równań ciągów liczbowych zamiast równaniami z JEDNĄ niewiadomą, przepisywanie 100 razy jednego równania typu y=5−x w metodzie podstawiania, co niczego nie wnosi do zadania i tylko wydłuża czas jego rozwiązywania itp. Ja się nie czepiam, tylko tępię okrężne metody serwowane uczniom przez naszych pożal śię Boże NIEKTÓRYCH belfrów (przepraszam, jeżeli kogoś uraziłem, bo są jeszcze dobrzy nauczyciele, chociaż to coraz rzadsze "przypadki") i pokazuję prostą droge do celu, a wiadomo − im prostsza droga, tym trudniej zbłądzić. Matma jest naprawdę prosta, tylko TŁUMACZONA JEST W OKRĘŻNY SPOSÓB I PO CHIŃSKU. A potem panika przed na sprawdzianie i maturą, bo uczeń zna tylko okrężne metody i nie wyrabia się czasowo z zadaniami. Taka jest smutna prawda i to widać na forum. Pozdrawiam Eta i nie czepiaj się mnie, bo ja nie czepiam się innych, czepiam się tylko POKRĘCONYCH METOD rozwiązywania zadań, bo 80 % zadań MOŻNA ZROBIĆ METODAMI PROSTSZYMI niż te serwowane przez szkołę.