mam problem ;/
AgA :): hej mam pytanko i potrzebna mi jest osoba która umie matematyke i dobrze tłumaczy

29 gru 15:12
magda: zależy czego dotyczy to pytanko?
29 gru 15:17
AgA :): nierówności kwadratowej
mam 10 zadan a ja z matma jestem na bakier i jej nie umiem chciałam zeby ktoś mógł mi je zrobic
i napisac dla czego tak a nie icnaczej sie je rozwiazuje
29 gru 15:35
Godzio:
Napisz zadania, mogę trochę potłumaczyć
29 gru 15:40
AgA :): a mogłabym wysłac na maila

było by może łatwiej i szybciej

29 gru 15:41
Godzio:
wrzuć na jakiś serwer

ja wracam za jakieś 8 min i się zabieramy
29 gru 15:42
AS: Godzio Ty nie bądź taki dobry,kto hurtem daje zadania
i rozwiążcie mi,to znaczy że samemu nic nie robi by
poprawić własne umiejętności matematyczne.
29 gru 15:47
Godzio:
Nie mam takiego zamiaru
 AgA
AgA chciała wytłumaczenia więc to postaram się zrobić
ewentualnie zrobię kilka przykładów,
29 gru 15:52
AgA :): no i sie mylisz as
bo mam pare zadan zrobionych ale z tego co widze i sprawdzałam na teori to nie jest to dobrze
zrobione
29 gru 15:53
29 gru 15:54
Godzio:
Od których zaczynamy ?
29 gru 15:54
AgA :): od 2.92?
29 gru 15:56
sssss: 2.92
a) zauwaz , ze kazda liczba podniesiona do kwadratu oraz powiekoszona o 5 zawsze bedzie wieksza
od 0. Wstaw sobie za x np −5 , −2 , 0 , 3 i to zauwazysz. Odpowiedz : x∊ℛ
pokombinuj tak z reszta z tych przykladow, cale te zadanie mozna zrobic tym sposobem
29 gru 16:01
AgA :): oki zaraz tak porobie i wstawie zdjecie to powiesz czy dobrze mysle oki
29 gru 16:04
Godzio:
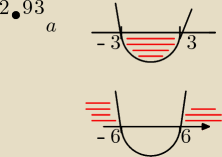
Ok, to z każdego zadania zrobię po 2−3 przykłady, mam nadzieje że tyle wystarczy
2.92
c) −2x
2 − 1 < 0 −− wyliczamy x
2
−2x
2 < 1 /:(−2)
| | 1 | |
x2 > − |
| −−− każda liczba podniesiona do kwadratu jest zawsze większa lub równa zero, |
| | 2 | |
więc ta nierówność jest spełniona przez każdego x
Odp: x ∊ R
| | 1 | |
d) 4x2 + 1 < 0 ⇒ 4x2 < −1 ⇒ x2 < − |
| teraz mamy podobną sytuację tyle że to jest |
| | 4 | |
sprzeczność, bo nie ma takiej liczby podniesionej do kwadratu która byłaby mniejsza od liczby
ujemnej
f) −3x
2 < 0 ⇒ x
2 > 0 −− przeczytam ten komentarz przy podpunkcie c), ta nierówność jest
spełniona dla każdego x bez 0 bo 0
2 = 0 a to nie jest większe od zera
2.93
a)x
2 − 9 < 0 gdy w przykładach pojawi się
2 i "−" to już niech lampka się zapala że
można skorzystać ze wzoru a
2 − b
2 = (a − b)(a + b) i tak właśnie będzie tu
x
2 − 3
2 < 0 ⇒ (x − 3)(x + 3) < 0 rysujesz oś, zaznaczasz miejsca zerowe (tu x = 3 lub
x = −3) i szkicujesz parabolę (jeśli przy najwyższej potędze jest liczba ujemna to ramiona są
do dołu jeśli dodatnia to do góry) i odczytujesz dla jakiego x, funkcja przyjmuje wartości
ujemne
I podajesz rozwiązanie x ∊ (−3,3)
| | 1 | | 1 | | 1 | | 1 | |
c) |
| x2 − 4 ≥ 0 ⇒ ( |
| x)2 − 22 ≥ 0 ⇒ ( |
| x − 2)( |
| x + 2) ≥ 0 |
| | 9 | | 3 | | 3 | | 3 | |
Jeśli nie widać od razu miejsc zerowych to po prostu przyrównujesz do 0 nawiasy
| 1 | | 1 | |
| x − 2 = 0 ⇒ |
| x = 2 ⇒ x = 6 |
| 3 | | 3 | |
| 1 | | 1 | |
| x + 2 = 0 ⇒ |
| x = −2 ⇒ x = −6 |
| 3 | | 3 | |
i znów szkicujesz parabolę z ramionami do góry i tutaj rozwiązanie jest dla wartości dodatnich,
czyli x ∊ (−
∞,−6)∪(6,
∞)
Zacznij analizować i porób kilka przykładów, dobrze gdybyś rozwiązania tutaj napisała to od
razu się sprawdzi, zaraz pokaże kolejne zadania
29 gru 16:10
Godzio: W ostatnim przykładnie powinny być oczywiście przedziały domknięte
(...,−6> ∪ [C[<6,..)
29 gru 16:13
AgA :): ja tak to robiłam
w zadaniu 2.92
a) x
2+5>0
x
2+5>0+5
5>0
x∊R
b)
−x@−1≤0/*(−1)
x
2+1≥0
x
2≥−1
c) mam zle
d)4x
+1<0
4x
2+1<0/;4
f)−3x
2<0/*(−1)
3x
2>0
3x
2>0
x∊R\{0}
czy w tym zadaniu mam dobrze to?
29 gru 16:18
Godzio:
jakie odpowiedzi w przykładach b), d), e) ?
a) i f) są ok
29 gru 16:21
AgA :): b)x∊R
d)∅
e)x∊N ?
29 gru 16:23
Godzio:
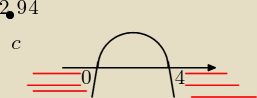
2.94 W tych przykładach wystarczy wyciągnąć wspólny czynnik przed nawias
| | 1 | |
a) 2x2 − x ≤ 0 ⇒ x(2x − 1) ≤ 0 miejsca zerowe to 0 i |
| , zaznaczasz na osi miejsca |
| | 2 | |
| | 1 | |
zerowe, parabola jest z ramionami do góry i odczytujesz rozwiązanie ⇒ x ∊ <0, |
| > |
| | 2 | |
c) 4x
− x
2 < 0 ⇒ x(4 − x) < 0 miejsca zerowe: 0 i 4, parabola jest z ramionami do
dołu bo przy najwyższej potędze jest liczba ujemna odp: x ∊ (−
∞,0) ∪ (4,
∞)
2.95 Na pierwszy rzut oka można wymnażać ale tutaj można też zauważyć że jest wspólny czynnik
który można wyłączyć przed nawias
b) (x − 3)
2 > (x − 3)(2x + 9) ⇒ (x − 3)
2 − (x − 3)(2x + 9) > 0 ⇒ (x − 3)(x − 3 − (2x + 9) ) >
0
(x − 3)(x − 3 − 2x − 9) > 0 ⇒ (x − 3)(−x − 12) > 0
Miejsca zerowe: x = 3 lub x = −12, parabola z ramionami do dołu bo x * (−x) =
−x
2
Odp: x ∊ (−12,3)
Te przykłady równie dobrze można wymnażać i liczyć deltę i pierwiastki
2.96 Też zrobię tylko jeden przykład, masz już gotowca wystarczy odczytać miejsca zerowe i
naszkicować parabole
c) 3(2 − x)(x + 4) ≤ 0 ⇒ miejsca zerowe: 2 i −4, parabola z ramionami do dołu bo (−x) * x =
−x
2
i po naszkicowaniu wartości ujemne są dla x ∊ (−
∞,−4> ∪ <2,
∞)
2.97 całe zadanie opiera się na dwóch wzorach skróconego mnożenia,
a
2 + 2ab + b
2 = (a + b)
2
a
2 − 2ab + b
2 = (a − b)
2
Natomiast jeśli ich nie zauważysz liczysz normalnie deltę i pierwiastki
| | 5 | |
d) 9x2 − 30x + 25 ≤ 0 → (3x − 5)2 ≤ 0 −− miejsce zerowe: 3x − 5 = 0 ⇒ 3x = 5 ⇒ x = |
| |
| | 3 | |
| | 5 | |
Nierówność spełniona tylko i wyłącznie dla x = |
| bo (...)2 nie może być ujemne ale może |
| | 3 | |
być zerem
f) −4x
2 + 12x − 9 ≥ 0 ⇒ −(4x
2 − 12x + 9) ≥ 0 ⇒
−(2x − 3)
2 ≥ 0 −− podobnie jak wyżej,
| | 3 | |
nierówność spełniona tylko dla x = |
| |
| | 2 | |
29 gru 16:27
Godzio:
| | 1 | |
W e) także brak rozwiązań będzie x2 ≤ − |
| −− to jest sprzeczność |
| | 2 | |
29 gru 16:28
AgA :): czli w b w zad. 2.94 bd tak
29 gru 16:34
Godzio:
tak,
29 gru 16:35
AgA :): w c)
4x−x2<0
x(4−x)<0
miejsca zerowe bd −1 4 i parabola w dół
29 gru 16:36
Godzio:
dokładnie tak, to jeszcze rozwiązanie podaj

29 gru 16:40
AgA :): a to nie koniec

ja myslałam ze to tak wystarczy
jak mam to dalej rozwiazac?
29 gru 16:42
Godzio: Trzeba podać rozwiązanie, tak jak w przykładach szkicujesz sobie parabole i odczytujesz
rozwiązanie, to zadanie by się skończyło gdyby było to równanie a nie nierówność
29 gru 16:51
AgA :): aha czyli to bd tak od (−7,−1) i (4+&) tak?
29 gru 16:53
AgA :): sorki tam miało byc od (−&,−1)
29 gru 16:54
Godzio:
Jeśli mówisz o c) to rozwiązanie będzie
(−∞,0)∪(4,∞)
Nie zauważyłem ale miejsca zerowe to 0 i 4 a nie −1
x(....) < 0 −−− tutaj miejscem zerowym jest 0 bo dla x = 0 całe wyrażenie się zeruje
29 gru 16:55
AgA :): sory ja sie walnełam juz miałam na mysli b)
jak juz wyłacze przed nawias to jest tak
i tu miejsce zerowbe bd 0 i 5 tak?
x∊(−&,0) (5+&) parabola w dół?
29 gru 16:59
Godzio: przyrównaj cały nawias do zera i sprawdź dla jakiego x będzie się zerował
| | 1 | | 5 | | 5 | |
dla 5 jest |
| * 5 − 5 = |
| − 5 = − |
| |
| | 2 | | 2 | | 2 | |
29 gru 17:01
AgA :): no to juz nic nei wiem dzis
29 gru 17:06
AgA :): aa juz wiem
29 gru 17:09
Godzio:
| 1 | | 1 | |
| x − 5 = 0 ⇒ |
| x = 5 ⇒ x = 10 −− to jest miejsce zerowe, |
| 2 | | 2 | |
Szukając miejsc zerowych przyrównujesz poszczególne czynniki do zera
| | 1 | | 1 | |
x( |
| x + 1)(2 + √2x)(x + |
| ) = 0 |
| | 2 | | 3 | |
| | 1 | | 1 | |
x = 0 lub |
| x + 1 = 0 lub 2 + √2x = 0 lub x + |
| = 0 |
| | 2 | | 3 | |
| | 2 | | √2 | | −2√2 | |
√2x = −2 ⇒ x = − |
| * |
| = |
| = − √2 |
| | √2 | | √2 | | 2 | |
| | 1 | |
Odp: x = 0, x = −2, x = − √2, x = − |
| |
| | 3 | |
29 gru 17:10
AgA :): a tutaj
−5x+x2≥0
x(−5x+x)≥0
i tutaj trzeba mnożyc przez 1?
29 gru 17:16
AgA :): 
29 gru 17:19
Godzio:
x(x − 5) ≥ 0
Nic więcej robić nie trzeba, teraz tylko naszkicować parabole i odczytać rozwiązanie
29 gru 17:21
AgA :): miejsa zerowe bd 0 i 5 i parabola z ramionami do góry bo najwyższa w potedze jest + tak?
29 gru 17:24
Godzio:
Tak, to teraz podaj rozwiązanie

29 gru 17:33
AgA :): x∊(−&,0> i <5,+&)
powiedz ze dobrze bo zaraz mnie szlak trafi

29 gru 17:35
Godzio: 

29 gru 17:38
AgA :): 
na reszcze moze coś zrozumiałam
mówie CI jestem noga zmatmy
ostatni podpunkt z tego zadania
−x
2−9x<0
−x(−x−9x)<0
miejsca zerowe −10 − 0 rammiona paroblloi w dół
x∊(−&,−10) i (0,+&)
29 gru 17:42
Godzio:
coś nie tak wyciągasz
−x(x + 9) < 0 skoro wyciągnęłaś minusa to w nawiasach on znika
przykłady:
−x2 + 5x = −x(x − 5)
−x2 − 4x = −x(x + 4)
29 gru 17:44
Godzio:
To jakie będą w końcu miejsca zerowe ?

0 i ?
29 gru 17:44
AgA :): aa no tak zapomniałam

czyli bd tak
−x(−x+9)<0
miejsca to 0 i 9 tak?
29 gru 17:46
Godzio:
Znów − nie znikł
 −
−x
2 − 9x = −x(x + 9)
29 gru 17:47
AgA :): no tak minus i minus daje +
ale to w koncu teraz jak bd?
29 gru 17:49
Godzio:
miejsca zerowe będą 0 i −9 i teraz zaznacz na osi i napisz rozwiązanie
29 gru 17:50
AgA :): parabola w dół prawda?(−&,−9) i (0,+&)
29 gru 17:51
Godzio:
ok

29 gru 17:51
AgA :): wreście

musze sobie przerwe zrobic na

wróce bd jeszcze

to mi pomożesz dalej

oki?
29 gru 17:53
Godzio:
wieczorem będę

koło 22 teraz uciekam
29 gru 17:54
AgA :): oki wiec i ja tak bd")
dzieki do usłyszenia wieczorem

29 gru 17:56

 było by może łatwiej i szybciej
było by może łatwiej i szybciej
 ja wracam za jakieś 8 min i się zabieramy
ja wracam za jakieś 8 min i się zabieramy
 AgA chciała wytłumaczenia więc to postaram się zrobić
ewentualnie zrobię kilka przykładów,
AgA chciała wytłumaczenia więc to postaram się zrobić
ewentualnie zrobię kilka przykładów,
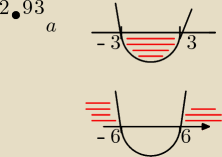 Ok, to z każdego zadania zrobię po 2−3 przykłady, mam nadzieje że tyle wystarczy
2.92
c) −2x2 − 1 < 0 −− wyliczamy x2
−2x2 < 1 /:(−2)
Ok, to z każdego zadania zrobię po 2−3 przykłady, mam nadzieje że tyle wystarczy
2.92
c) −2x2 − 1 < 0 −− wyliczamy x2
−2x2 < 1 /:(−2)
 2.94 W tych przykładach wystarczy wyciągnąć wspólny czynnik przed nawias
2.94 W tych przykładach wystarczy wyciągnąć wspólny czynnik przed nawias

 ja myslałam ze to tak wystarczy
jak mam to dalej rozwiazac?
ja myslałam ze to tak wystarczy
jak mam to dalej rozwiazac?





 na reszcze moze coś zrozumiałam
mówie CI jestem noga zmatmy
ostatni podpunkt z tego zadania
−x2−9x<0
−x(−x−9x)<0
miejsca zerowe −10 − 0 rammiona paroblloi w dół
x∊(−&,−10) i (0,+&)
na reszcze moze coś zrozumiałam
mówie CI jestem noga zmatmy
ostatni podpunkt z tego zadania
−x2−9x<0
−x(−x−9x)<0
miejsca zerowe −10 − 0 rammiona paroblloi w dół
x∊(−&,−10) i (0,+&)
 0 i ?
0 i ?
 czyli bd tak
−x(−x+9)<0
miejsca to 0 i 9 tak?
czyli bd tak
−x(−x+9)<0
miejsca to 0 i 9 tak?
 −x2 − 9x = −x(x + 9)
−x2 − 9x = −x(x + 9)

 musze sobie przerwe zrobic na
musze sobie przerwe zrobic na  wróce bd jeszcze
wróce bd jeszcze to mi pomożesz dalej
to mi pomożesz dalej  oki?
oki?
 koło 22 teraz uciekam
koło 22 teraz uciekam
