..
bart: Zbadaj przebieg zmiennosci funkcji
f(x)=|x2−6x+8|+|x2−6x+5|
29 gru 00:02
29 gru 00:04
bart: skad wiesz ze dla x ∊(−∞,1> i x∊<5,∞) bedzie ta sama wartosc?
29 gru 00:14
Godzio:
Odczytałem to, spróbuj to dokładnie przeanalizować
29 gru 00:15
Trivial: Podstaw sobie g(x) = x
2 − 6x + 8:
f(x) = |g(x)| + |g(x) − 3|
Rozpatrz, co się dzieje, gdy:
1. g(x) ∊ (−
∞, 0)
2. g(x) ∊ [0, 3]
3. g(x) ∊ (3, +
∞)
29 gru 00:16
bart: zapomnialem juz to wszystko
granica jakas, asymptoty>
29 gru 00:19
Trivial:
Dla przedziału:
1. obie ujemne:
f(x) = −g(x) − g(x) + 3 = −2g(x) + 3
2. jedna dodatnia, druga ujemna:
f(x) = g(x) − g(x) + 3 = 3.
3. obie dodatnie
f(x) = 2g(x) − 3
Pozostaje rozwiązanie przedziałów dla g(x) i podstawienie za g(x) wyrażenia które ukryliśmy na
początku.
29 gru 00:23
bart: co Ty mi tu teraz zasadziles?
29 gru 00:25
bart: Zajmnijmy sie teraz asymptotami i granicami
29 gru 00:26
Trivial: no to liczysz sobie limesy i już.
29 gru 00:31
bart: no ale to jest w bezwzglednej wartosci..
29 gru 00:33
bart: chociaz tak na chlopski rozum to tu ∞ i tu ∞ pomwinna byc..
29 gru 00:35
Trivial:
f(x) = |x
2 − 6x + 8| + |x
2 − 6x + 5|
Musisz najpierw zapisać bez użycia wartości bezwzględnej. Żeby tego dokonać robisz np. tak jak
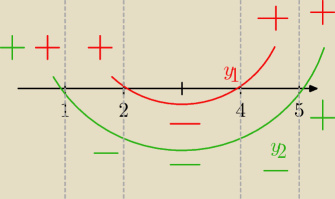
powiedziałem wcześniej, albo po prostu rysujesz sobie szkice tych dwóch funkcji i określasz
przedziały.
y
1 = x
2 − 6x + 8
Δ = 36 − 32 = 4
x ∊ {2, 4}
y
2 = x
2 − 6x + 5
Δ = 36 − 20 = 16
x ∊ {1, 5}
Rysujemy...
29 gru 00:45
Trivial:
Gdy obie funkcje są dodatnie, czyli w (−
∞, 1) i (5,
∞) f(x) wygląda tak:
f(x) = 2x
2 −12x + 13
W przedziałach <1, 2> i <4, 5> y
1 jest dodatnie, y
2 jest ujemne:
f(x) = 3.
W przedziale (2, 4) obie funkcje są ujemne:
f(x) = −2x
2 + 12x − 13.
Ot cała filozofia. Teraz dasz radę?
29 gru 00:50
bart: czyli os 0Y przetna tylko w przedizale (−
∞,1> w punkcjie (0,13)?
te dziubki tak na pewno beda tzn nawiasy?
29 gru 00:55
Trivial: Żeby sprawdzić, W którym punkcje jakakolwiek funkcja przecina oś Oy po prostu podstawiasz x =
0. Do tego nie trzeba nawet likwidować modułów.
29 gru 01:01
Trivial: Btw, co u ciebie oznacza zbadanie przebiegu zmienności funkcji?
29 gru 01:04
bart: dziedzina, asymptoty, granicamiejsca zerowe, punkt przeciecia z osia Y, badanie I i II
pochodnej, tableka, wykres, parzystosc i okresowosc
29 gru 01:07
Trivial: To to samo, co u nas.
29 gru 01:08
Trivial: to to samo co u nas.
29 gru 01:08
bart: mailem to we wrzesniu a juz to zapominam.. wkurza mnie to
29 gru 01:10
Trivial: Dziwne, jakieś opóźnienia są w wysyłaniu.
29 gru 01:10
bart: pochodna z pierwszego zalozenia to 4x−12
przyrownujemy do 0 i x=3 to czemu ta 3 nie jest miejscem zerowym?
29 gru 01:12
Trivial: To znaczy, że 3 jest ekstremum lokalnym. W tym wypadku minimum.
29 gru 01:14
Trivial: A..., makskimum, sry.
29 gru 01:14
bart: no to tez.. no ale sie uczylem ze jezeli ta 3 nie jest pierwiastkiem parzystej krotnosci to to
jest miejsce zerowe.. ale ta 3 nie nalezy do przedzialu wiec wgl mam sie z nia bawic?
29 gru 01:16
Trivial: No na wykresie, x=3 to maksimum lokalne. Hm.
29 gru 01:19
Trivial: Ah, nie myślę już o tak późnej godzinie. Nie należy do przedziału to raczej się odrzuca. Jak
się przyrówna do zera f'(x) w przedziale (2, 4) to też wyjdzie 3, czyli jest OK.
29 gru 01:21
bart: ato to wyjdzie mi dopiero w 3 zalozeniu tak? bo teraz−w pierwszym zalozeniu to ni chu chu
29 gru 01:22
bart: WIELKIE DZIEKI
!
mysle, ze juz sobie poradze
29 gru 01:24
Basia:
nie chcę Was dobijać, ale w tym konkretnym przypadku należy jeszcze zbadać ciągłość (i być może
różniczkowalność) w punktach
1,2,4,5
29 gru 01:28
Trivial: Tak w ogóle, to nie sprawdza się tylko, kiedy pochodna jest zerem, ale też kiedy jest ujemna a
kiedy dodatnia.
| | ⎧ | 2x2−12x+13; x∊(−∞,1)∪(5, ∞) | |
| f(x) = | ⎨ | 3; x∊<1,2>∪<4,5> |
|
| | ⎩ | −2x2+12x−13; x∊(2,4) | |
| | ⎧ | 4x−12; x∊(−∞,1)∪(5, ∞) | |
| f'(x) = | ⎨ | 0; x∊<1,2>∪<4,5> |
|
| | ⎩ | −4x+12; x∊(2,4) | |
29 gru 01:30
Trivial: To piszemy komentarz:
Ciągłość i różniczkowalność funkcji zbadana w pamięci. Wyszło OK.
29 gru 01:32
Basia:
zgadza się jest i ciągła i różniczkowalna, ale przypuszczam, że to wymaga jednak dowodu;
łatwy jest
29 gru 01:38
Trivial: Dobra...
Jak chcesz to sobie kończ to zadanie, ja idę spać.
Dobranoc.
29 gru 01:38
bart: a na co nam ujemna czy dodatnia pochodna?
29 gru 01:45
Basia:
na podstawie znaku pochodnej określa się czy funkcja jest rosnąca czy malejąca
a potem z tego dopiero wynika czy znalezione ekstremum to minimum czy maksimum
29 gru 02:04
bart: ano fakt, ale to z wykresu odczytuje, wiec juz zapomnialem o tym.. dzieki
29 gru 02:11
Monika: naszkicuj wykres funkcji log{2} x−2.Podaj dziedzinę funkcji,dla jakich argumentów funkcja
przyjmuje wartości ujemne
29 gru 08:56
bart: D∊x(2,∞)
ujemne przyjmuje dla x∊(2,3)
29 gru 10:33