Dla gofera Wafel: −3x(2+4x)≥0 wymnażamy i wychodzi: −6x−12x²≥0 żeby lepiej widzieć co tu mam ułożyłam liczby od najwyższy potęg do najmniejszych: −12x²−6x≥0 i z tego robimy delte Δ=b²−4ac Δ=(−6)²−4*(−12)*0 zero z tąd sie wzieło bo nie ma wyrazu c−−−> wg wzoru ogólnego funkcji y=ax²+bx+c Δ=36 i dalej wiadomo

Trivial: Że tak się zapytam. Po co tutaj wymnażać i wyliczać deltę? −3x(2+4x) ≥ 0

	1
−12x(x+		)≥0
	2

bart: coś czuje, że nie zaczai co zrobiłeś

Trivial: Bo wiesz, ja policzyłem deltę w pamięci i znalazłem pierwiastki!

Wafel: Dla tego moski bo robie to bardzo powoli bo tłumacze koleżance, chyba napisane jest że dla kogoś a nie dla was co nie?

Trivial: Tak naprawdę to wyłączyłem 4 przed nawias, co nie?

bart: no to tlumacz dalej.. zacznie rozpisywac (x−2)(x+3)(x+4)=0

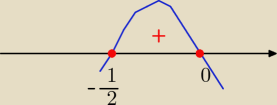
Eta: Wafel Nie wieź koleżanki na obiad : "z Gdańska do Sopotu przez Londyn", bo obiad Jej wystygnie wyznaczasz miejsca zerowe 3x=0 lub 2+4x=0 x=0 lub x= −¹₂ parabola ramionami do dołu odp: x€ < −¹₂, 0>

Wafel: 0=mx+y+1 || 0=3x−2y+4 to sa dane z zadania m musi być takie by te proste naprawde były różnowległe wg tego wzoru co Ci podałam to m musi sie równać temu co jest przed x ale zanim to określisz to musisz to ogarnąć, czyli po lewej stronie musi być y a po prawej cała reszta burdelu czyli: y=mx+1 || 2y=3x+4 jako że ma być y, a nie 2y(prosta po prawej), czy inne duperele to wykonujesz takie działanie by był tej jeden durny y, w tym wypadku dzielisz(ale tylko prosta po prawej) y=mx+1 || y=³₂x+2 jak mowiłam m ma być równe temu co przed x czyli w tym waypadku m=³₂ i teraz te proste sa rownoległe

Eta: k: y= −m −1 wsp. kier. a₁= −m l : y= ³₂x +2 wsp. kier. a₂= ³₂

	3
k || l <=>a1=a2 => −m= 32 => m= −
	2