wielomiany astral: wyznacz zbiór gdy

	x2 −3x+1
B ={ x∊R i		≥ 1}
	x2−1

Trivial:

x2 − 3x + 1
	≥ 1
x2 − 1

x2 − 3x + 1
	− 1 ≥ 0
x2 − 1

x2 − 3x + 1		x2 − 1
	−		≥ 0
x2 − 1		x2 − 1

x2 − 3x + 1 − x2 + 1
	≥ 0
x2 − 1

− 3x + 2
	≥ 0 / *(x2 − 1)2
x2 − 1

(x² − 1)(−3x + 2) ≥ 0

	2
(x − 1)(x + 1)*(−3)(x −		) ≥ 0
	3

	2
−3(x + 1)(x −		)(x − 1) ≥ 0
	3

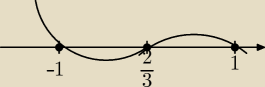
Rysujemy szkic wielomianu, wybieramy wartości powyżej lub równe 0 i mamy odpowiedź.

Trivial:

	2
x ∊ (−∞, −1> ∪ <		, 1>
	3

Trivial: No i jeszcze trzeba było wyznaczyć dziedzinę, o czym oczywiście zapomniałem. D = R − {±1} Czyli trzeba odrzucić jedynki z rozwiązania.

astral: dzieki