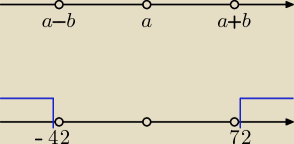
wartość bezwzględna astral: Opisz zbiór podany na rysunku za pomocą nierówności z wartością bezwzględną. doszedłem, że lewa strona to |x+15|, ale nie wiem jak wyznaczyć prawą?

astral: tzn wiem, że prawa strona to (42+72)/2 = 57, ale nie do końca rozumiem dlaczego własnie tak.

Jack: (−42+72)/2=15 |x−15|>57 https://matematykaszkolna.pl/strona/1652.html

Trivial: Jack te wartości trzeba odjąć a nie dodać.

Trivial: chyba?

astral: dobrze, 42 jest na minusie

Trivial: Aha, pomotało mi się. sorry.

astral: w kazdym razie dzięki

Jack:

Bogdan: |x − a| = b, |x − a| < b, |x − a| ≤ b, |x − a| > b, |x − a| ≥ b a to środek odcinka o współrzędnych na osi: a − b, x + b, b to odległość od liczby a na osi liczbowej.

	−42 + 72
Wyznaczamy środek odcinka o końcach: −42 i 72: a =		= 15
	2

b = 15 − (−42) = 72 − 15 = 57 Odp.: |x − 15| > 57

Bogdan: a to środek odcinka o współrzędnych na osi: a − b, a + b,