graniastosłupy cherry: Podstawą graniastosłupa prostego jest równoległobok o kącie ostrym α. Przekątne graniastosłupa są nachylone do płaszczyzny podstawy pod katami β i γ ( β < γ ), a wysokość graniastosłupa ma długość H. Oblicz objętość tego graniastosłupa.

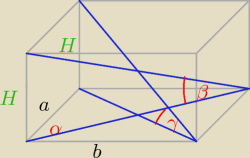
Godzio: e,f − przekątne podstawy

	e
ctgβ =		⇒ e = H * ctgβ
	H

	f
ctgγ =		⇒ f = ctgγ * H
	H

z tw. cos. a² + b² − 2abcos(180 − α) = e² ( cos(180 − α) = −cosα a² + b² − 2abcosα = f² − −−−−−−−−−−−−−−−−−−−−−−−− 4abcosα = e² − f²

	e2 − f2		H2(ctg2β − ctg2γ)
ab =		=
	4cosα		4cosα

	1
V = ab * sinα * H =		H3(ctg2β − ctg2γ)tgα
	4

ctg²β − ctg²γ = (ctgβ − ctgγ)(ctgβ + ctgγ) =

	sin(β − γ)		sin(β + γ)
−		*
	sinβsinγ		sinβsinγ

	1		sin(β − γ)sin(β + γ)
V = −		H3tgα
	4		sin2βsin2γ

Monika13: równoległobok o przekątnych A i B i kącie alfa między przekątnymi

Monika13: