zadanka
Eta: Zadanka dla chętnych

1) Pająk siedzi na środku krawędzi ściany pokoju ( w kształcie sześcianu)
i spostrzega w najdalej oddalonym kącie
muchę.
Posuwa się ku niej po
najkrótszej drodze ( po linii prostej).
Jaka jest wartość tej drogi do
muchy ?
2) Zadanie, które przedłożył Napoleon francuskim matematykom:
Dany okrąg o znanym środku i promieniu należy podzielić na 4 równe części.
Przy rozwiązywaniu zadania nie można posługiwać się linijką .

26 gru 17:16
dero2005:
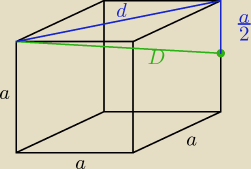
D =
32a
26 gru 19:03
dero2005:
droga zielona jest najkrótsza ale musimy założyć, że w pokoju nie były dawno sprzątane
pajęczyny
natomiast, gdy pająk będzie musiał chodzić po tynku to najkrótsza droga będzie niebieska =
= a(12+√2)
26 gru 19:18
R.W.17l: 2. Wyciąć okrąg, czyli koło będzie, zgiąć w pół a potem prostopadle. Wkleić i zaznaczyć
zagięcia na okręgu

26 gru 19:23
Bogdan:
Stwierdzenie dero2005: "natomiast, gdy pająk będzie musiał chodzić po tynku to najkrótsza
droga będzie niebieska" − nie jest prawdziwe. Istnieje inna droga, krótsza od niebieskiej.
26 gru 19:37
Eta:

26 gru 19:38
Trivial:

26 gru 19:41
Grześ: Ja wiem jak z tym pająkiem. Zrobie rysunek i coś pokaże


26 gru 20:01
Grześ:
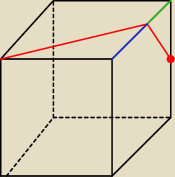
Zielony odcinek to x, a niebieski odcinek to a−x. Juz zapiszę funkcję, opisującą długośc tej
drogi.
26 gru 20:04
Grześ: Dł. Czerwonej drogi wynosi:
S=
√a2+x2+
√(a−x)2+a2
Teraz tylko myślę, jak ustalić najmniejszą wartość tej funkcji, czyli:
f(x)=
√a2+x2+
√(a−x)2+a2 , gdzie a jest stałą.
Ma ktoś pomysł?

26 gru 20:06
Eta:
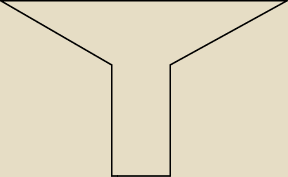
zad 3/ Na jaką najmniejszą liczbę części należy rozciąć daną na rys. figurę,
aby ułożyć z tych części kwadrat ?
Narysuj ten kwadrat po złożeniu z tych części.

26 gru 20:16
Grześ: Znaczy sie literówkę zrobiłem, funkcja ta ma postać:
f(x)=√14a2+x2+√(a−x)2+a2
26 gru 20:18
Grześ: | | a | |
na logikę x= |
| , tylko jak wykazać to obliczeniowo  Czy może niekoniecznie a/2   |
| | 2 | |
26 gru 20:19
Grześ: odświeżam, ma ktoś pomysł na policzenie minimalnej wartości tej funkcji


26 gru 20:30
Bogdan:
W zadaniu z pająkiem nie potrzeba obliczać minimalnej wartości żadnej funkcji, należy
obliczyć długość najkrótszej drogi między dwoma punktami.
26 gru 20:46
Grześ: nie wiem jak wyrazić tego minimum wart. Jedynie co moge zrobić, to program alpha policzył
minimum i wynosi ono dla x=0,3761a, czyli najkrótsza droga wynosi ok.:
S
min=1,79686a
Jakby ktos miał pomysł na jakiś normalny sposób wyliczeniowy, to ja z chęcią czekam

26 gru 20:46
Grześ: Ale Bogdan, masz jakieś uzasadnienie, gdzie dokładnie jest ta droga

Ja przyjąłem, że jest
gdzies punkt przecięcia oddalony o x.

26 gru 20:47
Bogdan:
Grześ − na razie wstrzymam się z podpowiedziami, nie chcę psuć zabawy Tobie i innym.

26 gru 21:00
26 gru 21:25
Grześ: Policzyłem Bogdan.
Najkrótsza droga wynosi:
Dobrze


26 gru 21:31
Bogdan:
Znam rozwiązanie

. Narysuj siatkę sześcianu i zaznacz na niej wskazane punkty,
zaznacz odcinek między tymi punktami, oblicz długość tego odcinka przyjmując długość
krawędzi sześcianu a.
26 gru 21:32
Godzio:
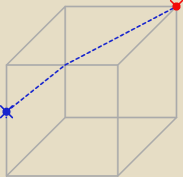
Moim zdaniem droga którą wskazał
Grześ jest najkrótsza, nie trzeba raczej uzasadniać że
tam jest
12a bo tylko wtedy droga jest najkrótsza
| √2 | | √5 | | √2 + √5 | |
| a + |
| a = |
| a |
| 2 | | 2 | | 2 | |
aczkolwiek mogę się mylić

26 gru 21:32
Grześ: Czyli akurat na ten pomysł wpadłem co Bogdan napisał. Czyli dobre obliczenia


26 gru 21:35
Bogdan:
Grześ − ok

26 gru 22:04
Eta:
Witam

26 gru 22:14
Grześ: Nie było mnie przez ten czas, sorki. Ale po napisaniu swojego postu wpadłem na taki fakt, że
można stworzyć dwie linie proste łączące te punkty w płaszczyźnie.
| | a | |
Jedna to przekątna prostokąta o wymiarach |
| na 2a , oraz prostokąta o wymiarach a na |
| | 2 | |
Wychodzą nad dwie odległości i wybieramy tą krótszą, czyli:
To jest poprawny tok rozumowania.


26 gru 22:47
Bogdan:
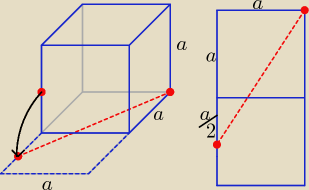
Długość odcinka oczywiście taka, jaka została podana przez
Etę 
26 gru 22:57
Grześ: Tak, jest jeszcze drugi przypadek, który ja wcześniej podałem


26 gru 22:59
Eta:

26 gru 23:02
Bogdan:
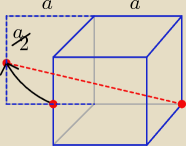
| | √17 | |
Tutaj d = a |
| , zadanie jednak polega na znalezieniu najkrótszej drogi, najkrótsza |
| | 2 | |
| | √13 | |
droga ma długość d = a |
| |
| | 2 | |
26 gru 23:17
AS: Uwaga do zadania 2
Podział przy pomocy samej linijki (bez zaginania) nie jest możliwy.
Można tego dokonać przy pomocy samego cyrkla i zaginania.
27 gru 11:23
AS:
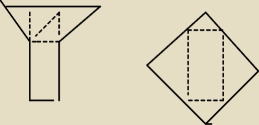
27 gru 13:39
Bogdan:
Uwaga do zadania 2.
Bez określenia proporcji odcinków, z których zbudowana jest figura, nie można rozwiązać
zadania. Proponuję
Eto narysować go na planszy z kratką (trochę roboty jest przy
kreśleniu kratki)

27 gru 15:50
Eta:
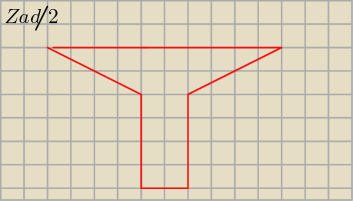
Witam
Bogdanie 
Teraz jest ok ?
27 gru 17:48
Bogdan:
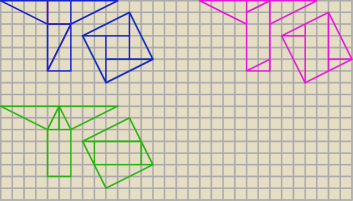
Teraz
Eto jest ok. Podaję przykłady rozcięcia figury.
27 gru 21:36
 1) Pająk siedzi na środku krawędzi ściany pokoju ( w kształcie sześcianu)
i spostrzega w najdalej oddalonym kącie muchę.
Posuwa się ku niej po najkrótszej drodze ( po linii prostej).
Jaka jest wartość tej drogi do muchy ?
2) Zadanie, które przedłożył Napoleon francuskim matematykom:
Dany okrąg o znanym środku i promieniu należy podzielić na 4 równe części.
Przy rozwiązywaniu zadania nie można posługiwać się linijką .
1) Pająk siedzi na środku krawędzi ściany pokoju ( w kształcie sześcianu)
i spostrzega w najdalej oddalonym kącie muchę.
Posuwa się ku niej po najkrótszej drodze ( po linii prostej).
Jaka jest wartość tej drogi do muchy ?
2) Zadanie, które przedłożył Napoleon francuskim matematykom:
Dany okrąg o znanym środku i promieniu należy podzielić na 4 równe części.
Przy rozwiązywaniu zadania nie można posługiwać się linijką .

 D =32a
D =32a





 Zielony odcinek to x, a niebieski odcinek to a−x. Juz zapiszę funkcję, opisującą długośc tej
drogi.
Zielony odcinek to x, a niebieski odcinek to a−x. Juz zapiszę funkcję, opisującą długośc tej
drogi.

 zad 3/ Na jaką najmniejszą liczbę części należy rozciąć daną na rys. figurę,
aby ułożyć z tych części kwadrat ?
Narysuj ten kwadrat po złożeniu z tych części.
zad 3/ Na jaką najmniejszą liczbę części należy rozciąć daną na rys. figurę,
aby ułożyć z tych części kwadrat ?
Narysuj ten kwadrat po złożeniu z tych części.

 Czy może niekoniecznie a/2
Czy może niekoniecznie a/2 




 Ja przyjąłem, że jest
gdzies punkt przecięcia oddalony o x.
Ja przyjąłem, że jest
gdzies punkt przecięcia oddalony o x. 


 I czy mój trop jest dobry
I czy mój trop jest dobry



 . Narysuj siatkę sześcianu i zaznacz na niej wskazane punkty,
zaznacz odcinek między tymi punktami, oblicz długość tego odcinka przyjmując długość
krawędzi sześcianu a.
. Narysuj siatkę sześcianu i zaznacz na niej wskazane punkty,
zaznacz odcinek między tymi punktami, oblicz długość tego odcinka przyjmując długość
krawędzi sześcianu a.
 Moim zdaniem droga którą wskazał Grześ jest najkrótsza, nie trzeba raczej uzasadniać że
tam jest 12a bo tylko wtedy droga jest najkrótsza
Moim zdaniem droga którą wskazał Grześ jest najkrótsza, nie trzeba raczej uzasadniać że
tam jest 12a bo tylko wtedy droga jest najkrótsza







 Długość odcinka oczywiście taka, jaka została podana przez Etę
Długość odcinka oczywiście taka, jaka została podana przez Etę 






 Witam Bogdanie
Witam Bogdanie  Teraz jest ok ?
Teraz jest ok ?
 Teraz Eto jest ok. Podaję przykłady rozcięcia figury.
Teraz Eto jest ok. Podaję przykłady rozcięcia figury.