| 1 | ||
y=− | x+4 | |
| 3 |
| 3 | 1 | |||
PKT ich przeciecia to: S( | ,3 | ) | ||
| 2 | 2 |
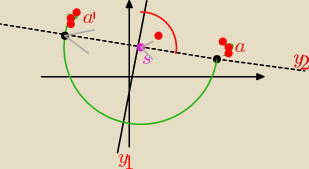 a'=b
y2=−1/3x+4
|sa|=|sa'| czyli można wektorowo (szare strzałki), ze wektor AS jest równy SA' (czyli SB)
pewnie umiesz liczyc wektory, to znajdź współrzędne wektora SB i przyrównaj do danych wektora
SA, czyli tak jak zrobił to Marcin W
i wylicz xB i yB
a'=b
y2=−1/3x+4
|sa|=|sa'| czyli można wektorowo (szare strzałki), ze wektor AS jest równy SA' (czyli SB)
pewnie umiesz liczyc wektory, to znajdź współrzędne wektora SB i przyrównaj do danych wektora
SA, czyli tak jak zrobił to Marcin W
i wylicz xB i yB


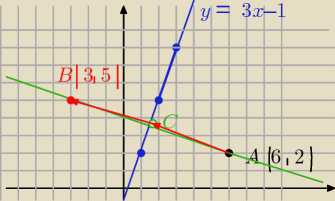 y = 3x−1 → a = 3
Szukamy równania prostej prostopadłej do danej przechodzącej przez punkt A
współczynnik a1 szukanej prostej musi spełniać warunki, żeby prosta była prostopadła
a*a1 = − 1
a1 = −1a = −13 = −13
podstawiamy wartości punktu A (6,2) i szukamy współczynnika b
2 = −13*6 + b
b = 4
y = −13x+4
Szukamy współrzędnych punktu C przecięcia się prostych
Porównujemy równania prostych
3x−1 = −13x+4
9x−3 = −1x+12
x = 1,5
y = 3*1,5−1 = 3,5
Punkt C (1,5;3,5)
Szukamy wektor AC → AC [1,5−6; 3,5−2] AC[−4,5;1,5]
Szukamy punktu B
Do punktu C dodajemy wektor AC
{1,5+(−4,5) ; 3,5+1,5}
punkt B (−3;5)
y = 3x−1 → a = 3
Szukamy równania prostej prostopadłej do danej przechodzącej przez punkt A
współczynnik a1 szukanej prostej musi spełniać warunki, żeby prosta była prostopadła
a*a1 = − 1
a1 = −1a = −13 = −13
podstawiamy wartości punktu A (6,2) i szukamy współczynnika b
2 = −13*6 + b
b = 4
y = −13x+4
Szukamy współrzędnych punktu C przecięcia się prostych
Porównujemy równania prostych
3x−1 = −13x+4
9x−3 = −1x+12
x = 1,5
y = 3*1,5−1 = 3,5
Punkt C (1,5;3,5)
Szukamy wektor AC → AC [1,5−6; 3,5−2] AC[−4,5;1,5]
Szukamy punktu B
Do punktu C dodajemy wektor AC
{1,5+(−4,5) ; 3,5+1,5}
punkt B (−3;5)