trojkaty Inka: Punkt P lezy wewnatrz prostokata ABCD. Wykaz ze suma pól trójkatów APD i BPC jest rowna sumie pól trojkatow APB i DPC. czarna magia hehe

Bogdan: Tu nie tylko nie ma czarnej magii, ale nie ma żadnej magii. Zadanie jest z poziomu szkoły podstawowej.

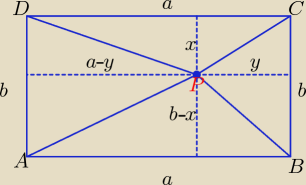
	1		1		1		1		1
PABP + PCDP =		*a*(b − x) +		*a*x =		ab −		ax +		*a*x =
	2		2		2		2		2

	1
=		ab
	2

	1		1		1		1		1
PDAP + PBCP =		*b*(a − y) +		*b*y =		ab −		by +		*b*y =
	2		2		2		2		2

	1
=		ab
	2

P_ABP + P_CDP = P_DAP + P_BCP co należało wykazać.

Bogdan: he he

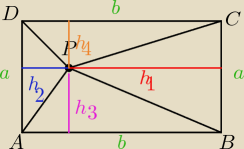Puch: Teza: P_ΔADP + P_ΔBPC = P_ΔAPB + P_ΔDPC Dowód: Zauważmy, że: h₁ + h₂ = b; h₃ + h₄ = a. Teraz:

	1		1		1		1
PΔADP + PΔBPC =		ah2 +		ah1 =		a(h1 + h2) =		ab
	2		2		2		2

	1		1		1		1
PΔAPB + PΔDPC =		bh3 +		bh4 =		b(h3 + h4) =		ab
	2		2		2		2

1		1
	ab =		ab ⇒ PΔADP + PΔBPC = PΔAPB + PΔDPC CND.
2		2

Inka: Banalne wiecie co swieta robia z czlowiekem hehe