Jak udowodnić, że równanie x^3-x+1=0 ma jedno rozwiązanie mniejsze od -1 ? ijac: Jak udowodnić, że równanie x³−x+1=0 ma jedno rozwiązanie mniejsze od −1 ?

ijac: up

Grześ: policz wartośc dla 0 oraz −1

Puch: Może poszukać wymiernych pierwiastków wielomianu, a potem zobaczymy.

Grześ: brak wymiernych pierwiastków

Grześ: tylko niewymierne są jakieś

Grześ: masz: W(x)=x³−x+1 Policz W(−1) oraz W(0)

Puch: Co z tego że wychodzi 1? ;s

Grześ: to znaczy, że pomiezy −1 a 0 znajduje sie pierwiastek tego równania Chociaż jeden

Puch: Trzeba dowieść, że pierwiastek jest mniejszy od −1, także chyba go nie będzie w (−1, 0).

Grześ: aj, źle spojrzałem, kurde

ijac: no właśnie, też sam się zakręciłem nie mam w ogóle pomysłu

Puch: Zapiszmy to może tak: x(x² − 1) = −1 Podzielmy przez niezerowy x.

	1
x2 − 1 = −
	x

	1
x2 = 1 −
	x

	x − 1
x2 =
	x

Czyli:

x − 1
	≥ 0 / * x2
x

x(x − 1) ≥ 0

Puch: Czy to do czegoś prowadzi?

Grześ: możesz wyliczyć zbiór x ale jak dla mnie to hmm.. nie wiem naprawdę

Zenek: x³ − x + 1 = 0 ⇔x(x−1)(x+1) = −1 ⇔ x³−x = −1 Jeżeli iloczyn trzech liczb ma być liczbą ujemną to a)wszystkie te liczby muszą być ujemne[x<−1] b)jedna z tych liczb musi być ujemna [ x ∊(0;1) ],ale wtedy x³ −x ∉ C;x³−x ∊ (−1;0) ≠ −1 Reasumując,jeżeli powyższe równanie posiada rozwiązanie(stwierdzenie owego faktu pozostawiam autorowi zadania) to musi być ono mniejsze niż −1

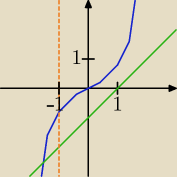
Bogdan: x³ − x + 1 = 0 x³ = x − 1 Naszkicujmy na jednym układzie współrzędnych wykresy: y = x³ i y = x − 1 Widzimy, że linie przecinają się w punkcie x < −1.

Puch: Jak widać, rozwiązanie było trywialne.