trygonometria nierównosć Chvdy: cos² (x−π/3) < 3/4

Chvdy: oczywiscie poproszę o rozwiazanie krok po kroku bo już sie w tym zgubiłem

Godzio:

	π		3		π
cos2(x −		) <		⇒ 4cos2(x −		) − 3 < 0
	3		4		3

	π
2(2cos2(x −		) − 1) − 1 < 0
	3

	2
2cos(2x −		π) < 1
	3

	2		1
cos(2x −		π) <
	3		2

	2		π		2		π
2x −		π =		+ 2kπ lub 2x −		π = −		+ 2kπ
	3		3		3		3

	π		π
x =		+ kπ lub x =		+ kπ
	2		6

	π		3π
x ∊ (		+ kπ ,		+ kπ)
	6		2

Chvdy: Zrobiłem przed chwila i wyszło mi troszkę inaczej. Zobacz: cos² (x−^π₃) < ³₄ − ^√3₂<cos (x−^π₃) < ^√3₂ przypadek 1 − ^√3₂<cos (x−^π₃) − ^5π₆ < cos (x−^π₃) lub ^5π₆ < cos (x−^π₃) x> − ^5π₆ +^2π₆ +2kπ lub x> ^5π₆ +^2π₆ +2kπ x> − ^3π₆ +2kπ lub x> ^7π₆ +2kπ x> − ^π₂ +2kπ Przypadek 2 cos (x−^π₃) < ^√3₂ x− ^π₃ < ^π₆ +2kπ lub x− ^π₃ < − ^π₆ +2kπ x< ^π₂ +2kπ lub x < ^π₆ +2kπ odpowiedź: x∊ (−π/2 +2kπ; π/6 +2kπ) lub (π/2 +2kπ; 7π/6 +2kπ) tak dobrze

Godzio: Rozwiązując taką nierówność:

	π		√3
cos(x −		) <		nie można zapisać:
	3		2

	π		π
x −		<		+ 2kπ −− nie zawsze musi się to zgadzać
	3		6

Odpowiedź jest ok, aczkolwiek można to skrócić do rozwiązania takiego jakie podałem

Chvdy: no ok . Czyli jest dobrze? bo w sumie jakby narysowac taki wykres(bez potęgi już) i go przesunąć to wtedy wyjda fajne przedziały. bo jeśli trafiło by mi sie cos podobnego na maturze to muszę wiedzieć a jeszcze mam pytanie gdzie w tym Twoim rozwiazaniu znikła jedna −1 i jeżeli usunąłeś kwadrat to wtedy wszystko powieksza sie o kolejny przypadek bo bedziemy mieli modół nałozony na tego cos. tak?

Godzio: U mnie ² zniknął bo skorzystałem ze wzoru: 2cos²x − 1 = cos2x

Godzio: Korzystając z tego wzoru (lub jego zamiennika 2cos²x − 1 = 1 − 2sin²x) można łatwo pominąć dużą ilość rozwiązań, u Ciebie wyszły 2 rozwiązania a u mnie tylko 1

Chvdy: ok już rozumiem. bo chciałem to robic metodą "tradycyjną" bez wzorów bo z nich korzystam przy bardzij skomplikowanych ale widzę że dużo zauważyłeś super. dzieki wielkie . ciekawi mnie tylko jakby to egzaminatorzy ocenili. a mógłbys mi wytłumaczyć jedna rzecz otóż gdy mam takie przypadki gdzie sin,cos,tg,cteg jakijś wartosci jesr równy większy mnijszy itd. od liczby ujemnej to wygląda to tak: np. sin(x)< −1/2 czyli sin(x)< −π/6 i π−(−π/6) czyli nie ma zadnej zmiany cos(x)<−1/2 czyli cos(x)< −5π/6 i 5π/6 czyli jest zmiana tg(x)<−1 czyli tg(x)< 3π/4 czyli jest zmiana ctg(x)<−1 czyli ctg(x)<3π/4 czyli jest zmina czy w każdym tego typu przypadku tak bedą zachodzić tak zmiany? poza sinusem gdzie zmiany nie ma

Chvdy: Isin(x)Isinx≤1/2 w przedziale <o;2π) rozpisałem to na 2 przypadki −1/2≤sin²x≤1/2 −√2/2≤sinx lub √2/2≥sinx −π/4+2kπ≤x lub x≤π/4+2kπ 5/4π≤x lub x≤3π/4 sin²x≤1/2 −√2/2 ≤sinx≤√2/2 i wyjdzie to samo więc ostatecznie x∊<0;π/4>lub <3π/4;5π/4> lub <7π/4;2π)

Chvdy: to też takie zadanko i nie jestem pewien czy dobrze

Godzio: ja Ci powiem znów, wole tak: 1^o sinx ∊ <0,π> ∪ {2π}

	1
sin2x ≤		/*2 / − 2sin2x
	2

0 ≤ 1 − 2sin²x

	π
0 ≤ cos2x ⇒ x ∊ <0,		> ∪ {2π}
	4

2^o sinx ∊ (π,2π)

	1
−sin2x ≤
	2

1 − 2sin²x ≤ 2 cos2x ≤ 2 ⇒ x ∊ (π,2π)

	π
Odp: <0,		> ∪ (π,2π) ∪ {2π} − trochę inne rozwiązanie mi wyszło niż u Ciebie, zaraz
	4

sprawdzę jeszcze

Godzio:

	π
Nie widzę błędu, odpowiedź można zapisać: <0,		> ∪ (π,2π>
	4

Chvdy: w drugim przypadku ten x∊(π,2π) bo π z dziedziny a 2π bo cos2x ≤ 2 ⇒ x≤ 2π (kąt 360) i czy mógłbys odpowiedzieć mi na to pytanie dotyczące zmian w sin,cos,tg,ctg? jak myślisz skad jest ta rozbieżność w naszych wynikach? wiem że Twoje są na pewno dobre ale nie wiem czemu

Godzio: przy sinusie, tg i ctg, po prostu kąt jest ujemny a przy cosinusie rozwiązanie trzeba przesunąć o π np.

	√2
cosx = −
	2

	π		π
x = π −		+ 2kπ lub x = − (π −		) + 2kπ
	4		4

reszta jest normalnie tgx = −1

	π
x = −		+ kπ
	4

ctgx = −1

	π
x = −		+ kπ
	4

	1
sinx = −
	2

	π		π
x = −		+ 2kπ lub x = π − (−		) + 2kπ
	6		6

Godzio: Z tego co widzę, ty rozwiązujesz tak że po prostu opuszczasz sobie funkcję, a tak nie można jak masz zwykła nierówność, najlepiej na boku rozwiązać sobie to samo tylko że jako równanie, znajdziesz w ten sposób punkty przecięcia, a następnie naszkicować sobie od ręki wykres i odczytać rozwiązanie, mając te punkty będzie to bardzo proste

Godzio: Wiesz co, moje rozwiązanie nie jest dokładnie poprawnie zaraz poprawie, w Twoim jest mały błąd chyba

Bogdan:

	π		3
cos2(x −		) −		< 0,
	3		4

	π		√3		π		√3
[cos(x −		) +		] [cos(x −		) −		] < 0,
	3		2		3		2

	π
na rysunku t = x −		(w zasadzie nie ma potrzeby stosować podstawienia,
	3

wprowadziłem je ze względu na pewną trudność tworzenia napisów z nawiasami na rysunku).

	√3		π		√3
−		< cos(x −		) <
	2		3		2

Po naszkicowaniu wykresów funkcji:

	π		√3		√3
y = cos(x −		) oraz prostych y = −		i y =
	3		2		2

dla ustalenia przedziałów spełniających nierówność, rozwiązujemy równania:

	π		√3		π		√3
cos(x −		) = −		oraz cos(x −		) =
	3		2		3		2

	π		π		π		π
(1) cos(x −		) = −cos		oraz (2) cos(x −		) = cos
	3		6		3		6

	π		5π
(1) cos(x −		) = cos
	3		6

	π		5π		π		5π
(1) x −		=		+ k*2π lub x −		= −		+ k*2π
	3		6		3		6

oraz

	π		π		π		π
(2) x −		=		+ k*2π lub x −		= −		+ k*2π
	3		6		3		6

Stąd:

	7		1
(1) x =		π + k*2π lub x = −		π + k*2π
	6		2

oraz

	1		1
(2) x =		π + k*2π lub x =		π + k*2π
	2		6

Ostatecznie rozwiązaniem nierówności jest:

	1		1		1		7
x∊(−		π + k*2π,		π + k*2π)∪(		π + k*2π,		π + k*2π)
	2		6		2		6

Chvdy: czyli jeśli pojawią mi sie w zadaniu 2(albo wiecej) funkcje np ten IsinusxI* sinusx albo jakis do kwadratu(bo wtedy też są 2 bo się mnoży ) to polecasz/karzesz kombinować z wzorami? bo to dla mnie ważne bo nie mam kogos kto by mnie nakierował. jesli tak jest to wtedy takie proste będe rozwiazywać normalnie a składające sie z kilku funkcji albo ewidentnie na wzór skorzystam z wzorów.

Chvdy: ja juz sam nie wiem jak to ma byc jestem pewnien że rozwiązanie Godzia w zadaniu z sinusem jest dobrze( tak jest w odpowiedziach w ksiazce) ale nie mam pojęcia skad te rozbierzności w naszych rozwiązaniach

Godzio: Wzory nie są konieczne, ale upraszczają dosyć rozwiązanie dla ćwiczeń, postaraj się:

	x		x		5
sin4		+ cos4		=
	3		3		8

	4x		1
sprowadzić do postaci cos		= −
	3		2

Godzio: Jak zrobisz to Ci później sprawdzę, teraz lecę i będę wieczorem

Chvdy: a według np. tego 1577 dla ctg też zmieniamy. więc jak to ma byc wkońcu?

Chvdy: wyszło mi tylko że sin4x/3 = −1/2 najpierw rozbiłem te 4 potęgi na sin²*sin² a później jednynka trygonometryczna 2 użycia(zeby rozbić) póxnij połaczyłem jedynką sin² i cos² przeniosłem na druga strone i już miałem wtedy po prawej −1/2 a po lewej −2cos² x/3*sin² x/3= − 1/2 nie wiem jak zrobic żeby był ten cosinus.

Godzio: co do tego ctg co wysłałaś tam Jakub przesunął rozwiązanie o 180^o, to akurat nie jest konieczne bo

	2		π
x =		π + kπ = −		+ kπ − po za tym tamto zadanie mówi o rozwiązaniu w przedziale w
	3		3

którym nie zawierają się rozwiązania ujemne i dlatego tak jest

Godzio:

x
	= t dla sprawniejszego zapisu
3

	5
sin4t + cos4t =
	8

	5
(sin2t + cos2t)2 − 2sin2tcos2t =
	8

	5
1 − 2sin2tcos2t =		/ * 2
	8

	5
2 − 4sin2tcos2t =
	4

	5
2 − (2sintcost)2 =
	4

	5
2 − sin22t =		/ * 2
	4

	5
4 − 2sin22t =
	2

	5
3 + 1 − 2sin22t =
	2

	1
cos4t = −
	2

	4x		1
cos		= −
	3		2

sprawdź i poszukaj błędu

Chvdy: ok masz racje z tymi zminami źle sobie popatrzyłem. czyli zminia sie tylko przy cosinusie. wszysto teraz mi się ułożyło jak to rozpisałeś. strasznie dużo kombinowania było i dlatego sie zgubiłem. patrzyłeś na rozwiązanie zadania przez Bogdana?

Godzio: Zerknąłem a co ?

Chvdy: no i własnie ja juz sam nie wiem co i jak bo to z sinusem 100% jest dobrze i według tego ten spoób powinien pasowac do tego z cos. ale wychodza 2 różn rozwiązania niby kawałek jest wspólny ale jednak jest pewna różnica

Godzio: A masz do tego odpowiedzi ?

Chvdy: no własnie nie i to jest najgorsze ze nawet nie mam jak sprawdzić jutro poszukam jakiegos analogicznego z odpowiedzią i spróbuje rozwiązać na 2 sposoby z wzorów i i rozpisując wszystko. i wtedy się dowiem co i jak

Godzio: Wiesz co, ja naniosę poprawkę do mojego rozwiązania bo widzę że zły przedział zrobiłem, chciałem w pamięci i nie wyszło

	π		7π
x ∊ (		+ kπ,		+ kπ)
	2		6

Godzio: sprawdź czy rozwiązania Bogdana się nie pokryją może akurat jak coś nie wyjdzie to napisz to sobie to rozpisze i sprawdzę

Chvdy: a narysuj sobie wykres cos(x−π/3) <3/4 ja tak zrobiłem . i wtedy zgdzały mi sie te moje wyniki bo teraz masz tak jakby wziętą pod uwagę jedną część cosinusa.

Godzio: Te Twoje rozwiązania pokrywają się z moimi to już sprawdzałem

Chvdy: bo ja rozwiązałem tak jak Bogdan

Godzio: Oba są dobrze, moje rozwiązanie pokrywa się z Twoim i Bogdana

Chvdy: znaczy mam tak jak on . tylko Ty masz ten przedział x∊(π/2 +kπ; 7π/6 +kπ) i rózni nas brak jednej częśc i to że ja mam 2kπ

Godzio: Moje rozwiązanie to x∊(π/2 +kπ; 7π/6 +kπ) Twoje: x∊ (−π/2 +2kπ; π/6 +2kπ) lub (π/2 +2kπ; 7π/6 +2kπ) i teraz ja przesuwam swoje: (π/2 +kπ; 7π/6 +kπ) = (−π/2 + kπ, π/6 + kπ) Więc oba są poprawnie jak widać, moje jest jedynie skrócone

Chvdy: ok zgadza sie narysowałem wszystko jeszcze raz popatrzyłem na Twoje i moje i pokrywa sie. aż mi ulżyło

Chvdy: a masz jakieieś podobne zadania do tego z tym sinusem? bo musze to przećwiczyć i załapać i nabyc sprytu w stosowaniu wzorów kiedy tak a kiedy nie

Godzio: Wiesz co, wpisz sobie tutaj w "wyszukaj" hasło "trygonometria" na pewno coś znajdziesz

Chvdy: a mam jeszcze 2 zadania. tgx≥ctgx narysowałem i wiadomo że π/4 jest dla tg i ctg 45 wiec będzie to ich punkt przeciecia rozwiazanie to x∊<π/4 +kπ;π/2+kπ) tak? i drugie zadanie nie wiem czy sie zgubiłem w nim czy co ale jest takie − √2/2 < sin(3x−π/4)≤ √3/2 Przypadek 1 Przypadek 2 −√2/2<sin(3x−π/4) sin(3x−π/4)≤ √3/2 −π/4+2kπ<3x −π/4 lub 5π/4 +2kπ< 3x− π/4 3x−π/4 ≤ π/3 +2kπ lub 3x−π/4 ≤ 2π/3 +2kπ 2/3kπ<x 6π/12+2/3kπ<x x≤ 7π/36 +2/3kπ lub x≤ 11π/36 +2/3kπ nie mam pojęcia czy do tego momentu jest dobrze i jak teraz wyznaczyc przedziały.

Godzio:

	√2
dla −
	2

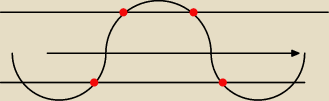
	π		π		π		5π
3x −		= −		+ 2kπ lub 3x −		=		+ 2kπ
	4		4		4		4

	2		π		2
x =		kπ lub x =		+		kπ
	3		2		3

	√3
dla
	2

	π		π		π		2π
3x −		=		+ 2kπ lub 3x −		=		+ 2kπ
	4		3		4		3

	7		2		11		2
x =		π +		kπ lub x =		π +		kπ
	36		3		36		3

	2		7		2		11		2		π		2
x ∊ (		kπ,		π +		kπ) ∪ (		π +		kπ,		+		kπ)
	3		36		3		36		3		2		3

Mam nadzieję że się nie pomyliłem