geometria grander: Czworokątną działkę podzielono na cztery części wzdłuż przekątnych. Powierzchnie trzech z tych działek wynoszą 120m kw., 200m kw., 300m kw. Pole całej działki wynosi:

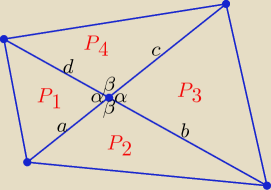
Bogdan: β = 180^o − α, sinβ = sin(180^o − α) = sinα

	1
P1 = 120 ⇒		ad*sinα = 120
	2

	1		1
P2 = 200 ⇒		ab*sinβ = 200 ⇒		ab*sinα = 200
	2		2

	1
P3 = 300 ⇒		bc*sinα = 300
	2

	1		1
P4 =		cd*sinβ =		cd*sinα
	2		2

	1		1		1		1
Zauważamy, że:		ad*sinα *		bc*sinα =		ab*sinβ *		cd*sinα
	2		2		2		2

	P1 * P3
czyli: P1 * P3 = P2 * P4 ⇒ P4 =
	P2

	120 * 300
W tym zadaniu: P4 =		= ...
	200