logarytmy, trudne^^ grey: f(x)= |2^|log_1/2x|−4|... mógłby ktoś wytłumaczyć, jak robi się zadania tego typu? Byłbym wdzięczny... rozumiem, że x>0... dalej nie mam pojęcia dlatego chce się nauczyć, a sam nie mam pomysłu.. pewnie trzeba rozpatrzyć log_1/2x≥0 i log_1/2x<0.. ale nie wiem jak zmienia się wtedy to co jest w wartości bezwzględnej..

grey:

⎧	|2log1/2x−4| log1/2≥0
⎩	|2−log1/2x−4| log1/2<0

grey: log_1/2x>0 i tam samo na dole

grey: ?

grey: odświeżam..

Godzio: chodzi o wykres ?

Marcin W: moglby pewnie jak bedzie jakies polecenie do twojego zadania. Co trzeba z tą funkcją zrobic ? narysować?

grey: tak, narysować

Jack: spróbuj rozpatrzyć możliwości. Zacznij od tego modułu wewnątrz.

grey: ⎧ |2^log_1/2x−4| log1/2≥0 ⎩ |2^−log_1/2x−4| log1/2<0

⎧	1/x−4
⎩	x−4	? .. yy

grey: i wartości | |

Godzio: Zaraz Ci to narysuje

Godzio: D = (0,∞)

	⎧	|2log1/2x − 4| gdy log1/2x ≥ 0
f(x) =	⎨
	⎩	|2−log1/2x − 4| gdy log1/2x < 0

	⎧	|2−log2x − 4| gdy x ≤ 1
f(x) =	⎨
	⎩	|(12)log1/2x − 4| gdy x > 1

	⎧	|1x − 4| gdy x ∊ (0,1)
f(x) =	⎨
	⎩	|x − 4| gdy x > 1

Godzio: Aj, zapomniałem o przesunięciu ten fragment hiperboli przesuń o 4 jednostki w dół, i to co będzie znajdować się poniżej osi OX odbij do góry

grey: dzięki

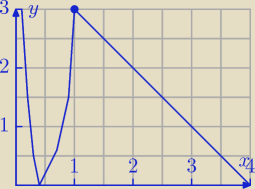
Godzio: W przybliżeniu będzie coś takiego

ziomek: chuj ci w dupe chodzi do gimbazy i tazkego nie mam