pilne
marlena: trójkat o bokach długości 15,20 i 25 obracamy wokół najdłuzszego boku i otrzymujemy bryłę
złożoną z dwóch stożków o wspólnej podstawie. objetość tej bryły jest równa
19 gru 11:41
Godzio:
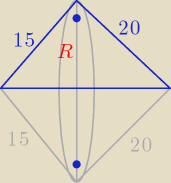
| R * 25 | | 15 * 20 | |
| = |
| ⇒ R = 12 |
| 2 | | 2 | |
R
2 + H
12 = 20
2 ⇒ H
12 = 256 ⇒ H
1 = 16
R
2 + H
22 = 15
2 ⇒ H
22 = 81 ⇒ H
2 = 9
| | 1 | | 1 | |
V = V1 + V2 = |
| πR2(H1 + H2) = |
| π * 144 * 25 = 1200π |
| | 3 | | 3 | |
19 gru 11:52
19 gru 11:54
marlena: dziekuje bardzo
19 gru 12:04
Jan: nie za bardzo rozumiem jak zostało wyliczone R, sorry że się wtrącam ale korzystam z cudzych
zadanek żeby się trochę poduczyć a tego nie rozumiem do końca
19 gru 12:06
Alberttynka:
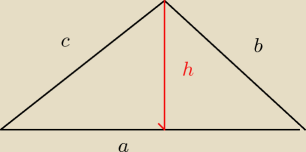
a=25 ,b=15 ,c=20 ;ΔABC−prostokątny
| | b2*c2 | |
V=13πh2a ⋀ h2 = |
| |
| | b2 + c2 | |
19 gru 12:32
Jan: ok już kumam, ja bym nie wpadł tak szybko że ten trójkąt, który obracamy, jest prostokątny
a proporcja oczywiście jest z podobieństwa trójkątów
19 gru 12:41