Punkt A jest jednym z wierzchołków trójkąta. Anka: Witam, Punkt A(−2,5) jest jednym z wierzchołków trójkąta równoramiennego ABC, w którym |AC|=|BC|. pole tego trójkąta jest równe 15. BC jest zawarty w prostej o równaniu y=x+1. Oblicz współrzędne wierzchołka C. Proszę o pomoc i dziękuję za wszystkie wskazówki.

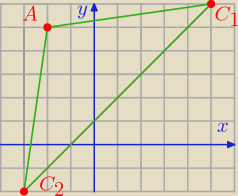
Godzio: Odległość prostej od punktu A to wysokość trójkąta, A(−2,5) x − y + 1 = 0

	| −2 − 5 + 1|		6√2
d =		=		= 3√2
	√2		2

	3√2 * |BC|
P =		= 15 ⇒ |BC| = 5√2 ( |BC| = |AC| )
	2

|AC| = 5√2 /² (x_C − x_A)² + (y_C − y_A)² = 50 punkt C należy do prostej y = x + 1 (x_C + 2)² + (x_C + 1 − 5)² = 50 x_C² + 4x_C + 4 + x_C² − 8x_c + 16 = 50 2x_C² − 4x_C − 30 = 0 x_C² − 2x_C − 15 = 0 (x_C − 5)(x_C + 3) = 0 x_C = 5 lub x_C = −3 y_C = 6 lub y_C = −2 Odp: C(5,6) lub C(−3,−2) − wiadomo że jeśli C(5,6) to B(−3,−2) tylko nie jestem pewien czy np. C(5,6) powinno się odrzucić ale chyba nie

nimkaa: jedno z Twoich C to bedzie B zalezy jak na rysunku oznaczysz